SEKILAS SPSS
SPSS adalah sebuah
program komputer yang digunakan untuk analisis statistik. Antara 2009 dan
2010 vendor utama untuk SPSS disebut PASW (Predictive Analytics Software)
Statistik, sementara isu-isu hak cipta nama itu diselesaikan. . [1]
Perusahaan mengumumkan 28 Juli 2009 itu diakuisisi oleh IBM untuk US $ 1,2
miliar [2] Pada Januari 2010, itu menjadi “SPSS: Sebuah Perusahaan IBM”.
Statistik Program
SPSS (awalnya, Paket Statistik untuk Ilmu Sosial) diluncurkan pada versi
pertama pada tahun 1968 setelah dikembangkan oleh Norman H. Nie dan C. Hadlai
Hull. Norman Nie kemudian sebuah pascasarjana ilmu politik di Stanford
University, dan sekarang Profesor Riset di Departemen Ilmu Politik di Stanford
dan Profesor Emeritus Ilmu Politik di Universitas Chicago [3]. SPSS adalah
salah satu program yang paling banyak digunakan untuk analisis
statistik dalam ilmu sosial. Hal ini digunakan oleh peneliti pasar,
peneliti kesehatan, perusahaan survei, pemerintah, peneliti pendidikan,
organisasi pemasaran dan lain-lain. Manual SPSS asli (Nie, Bent &
Hull, 1970) telah digambarkan sebagai salah satu “buku sosiologi yang paling
berpengaruh” [4] Selain analisis statistik., Manajemen data (seleksi kasus,
file membentuk kembali, membuat data turunan) dan data dokumentasi (kamus
metadata disimpan di datafile itu) adalah fitur dari software dasar.
Statistik disertakan dalam perangkat lunak dasar:
Statistik Deskriptif: Tabulasi silang, Frekuensi, Descriptives, Explore, Ratio
Statistik Deskriptif
Bivariat statistik: Berarti, t-test, ANOVA, Korelasi (bivariat, parsial,
jarak), tes nonparametrik
Prediksi untuk hasil numerik: regresi linier
Prediksi untuk mengidentifikasi kelompok: analisis faktor, analisis cluster
(dua-langkah, K-berarti, hirarkis), Diskriminan
Banyak fitur SPSS dapat diakses melalui menu pull-down atau dapat diprogram
dengan bahasa perintah sintaks proprietary 4GL.sintaks pemrograman Komando
memiliki keunggulan reprodusibilitas; menyederhanakan tugas yang berulang, dan
menangani manipulasi data yang kompleks dan analisis. Selain itu, beberapa
aplikasi yang kompleks hanya dapat diprogram dalam sintaks dan tidak dapat
diakses melalui struktur menu.Antarmuka menu pull-down juga menghasilkan
sintaks perintah, ini dapat ditampilkan dalam output meskipun setting default
harus diubah untuk membuat sintaks terlihat bagi pengguna, atau dapat
disisipkan ke dalam sebuah file dengan menggunakan sintaks “paste” tombol
ini dalam menu masing-masing. Program dapat dijalankan secara interaktif,
atau tanpa pengawasan menggunakan Fasilitas Kerja Produksi
disediakan. Selain itu sebuah “makro” bahasa dapat digunakan untuk menulis
bahasa perintah subrutin dan ekstensi programabilitas Python dapat mengakses
informasi dalam kamus data dan data dan dinamis membuat program perintah
sintaks. The Python programabilitas ekstensi, yang diperkenalkan pada SPSS
14, menggantikan SAX Basic yang kurang fungsional “script” untuk sebagian besar
tujuan, meskipun SaxBasic tetap tersedia. Selain itu, ekstensi Python
memungkinkan SPSS untuk menjalankan salah satu statistik dalam paket perangkat
lunak bebas R. Dari SPSS versi 14 dan seterusnya dapat digerakkan secara
eksternal oleh Python atau program VB.NET menggunakan diberikan
“plug-in”.
SPSS tempat kendala pada struktur file internal, tipe data, pengolahan data dan
pencocokan file, yang bersama-sama jauh mempermudah pemrograman. dataset
SPSS memiliki struktur tabel 2 dimensi dimana baris biasanya merupakan kasus
(seperti individu atau rumah tangga) dan kolom mewakili pengukuran (seperti
usia, jenis kelamin atau pendapatan rumah tangga).Hanya 2 tipe data
didefinisikan: numerik dan teks (atau “string”).Semua proses data terjadi
secara berurutan kasus per kasus melalui file. File dapat dicocokkan
satu-ke-satu dan satu-ke-banyak, tapi tidak banyak-ke-banyak.
User interface grafis memiliki dua pandangan yang dapat diaktifkan dengan
mengklik salah satu dari dua tab di kiri bawah dari jendela SPSS. The
‘Data View’ menampilkan tampilan spreadsheet dari kasus-kasus (baris) dan
variabel (kolom). Tidak seperti spreadsheet, sel-sel data hanya dapat
berisi angka atau teks dan formula tidak dapat disimpan dalam sel-sel
ini.menampilkan The ‘Lihat Variabel’ kamus metadata di mana setiap baris
mewakili sebuah variabel dan menampilkan nama variabel, label variabel, nilai
label (s), lebar cetak, jenis pengukuran dan berbagai karakteristik
lainnya. Sel-sel di kedua tampilan dapat diedit secara manual, menentukan
struktur file dan memungkinkan entri data tanpa menggunakan sintaks perintah. Hal
ini mungkin cukup untuk dataset kecil. Dataset yang lebih besar seperti
survei statistik lebih sering dibuat dalam perangkat lunak entri data, atau
dimasukkan selama computer-assisted personal wawancara, dengan pemindaian dan
menggunakan pengenalan karakter optik dan perangkat lunak menandai pengakuan
optik, atau dengan menangkap langsung dari kuesioner online. Dataset ini
kemudian dibaca ke dalam SPSS.
SPSS dapat membaca dan menulis data dari file teks ASCII (termasuk file
hirarkis), paket statistik lainnya, spreadsheet dan database. SPSS dapat
membaca dan menulis ke tabel database eksternal relasional melalui ODBC dan
SQL.
output statistik adalah format file proprietary (file *. SPV, mendukung tabel
poros) yang, selain penampil dalam paket, seorang pembaca yang berdiri sendiri
dapat didownload. Output proprietary dapat diekspor ke teks atau Microsoft
Word. Atau, output dapat ditangkap sebagai data (menggunakan perintah
OMS), sebagai teks, teks tab-delimited, PDF, XLS, HTML, XML, dataset SPSS atau
berbagai macam format gambar grafis (JPEG, PNG, BMP dan EMF).
Logo SPSS digunakan sebelum penggantian nama pada Januari 2010.
Add-on modul memberikan kemampuan tambahan. Modul-modul yang tersedia
adalah:
SPSS Programmability Extension (ditambahkan pada versi 14).Memungkinkan Python,
R, dan. NET kontrol pemrograman SPSS.
SPSS Validasi Data (ditambahkan pada versi 14). Memungkinkan pemrograman
pengecekan logis dan pelaporan nilai-nilai mencurigakan.
SPSS Regresi Model – regresi logistik, regresi ordinal, regresi logistik multinomial,
dan model campuran.
SPSS Advanced Models – GLM Multivariate dan mengulangi langkah-langkah ANOVA
(dihapus dari sistem dasar dalam versi 14).
SPSS Klasifikasi Pohon. Membuat pohon klasifikasi dan keputusan untuk
mengidentifikasi kelompok dan memprediksi perilaku.
Tabel SPSS. Memungkinkan kontrol user-defined output untuk laporan.
SPSS Exact Tests. Memungkinkan pengujian statistik pada sampel kecil.
SPSS Kategori
SPSS Trends
SPSS Conjoint
Hilang SPSS Analisis Nilai. Wikipedia Imputasi regresi berbasis.
SPSS Peta
SPSS Kompleks Sampel (ditambahkan pada Versi 12).Menyesuaikan untuk
stratifikasi dan clustering dan bias pemilihan sampel lainnya.
SPSS Server adalah sebuah versi dari SPSS dengan klien / arsitektur
server. Hal itu beberapa fitur tidak tersedia pada versi desktop, seperti
fungsi penilaian (Scoring fungsi tersebut dimasukkan ke dalam versi desktop
dari versi 19).
Versi
Awal SPSS versi dirancang untuk pemrosesan batch di mainframe, termasuk
misalnya IBM dan versi ICL, awalnya menggunakan kartu menekan untuk
input. Sebuah menjalankan pengolahan membaca file perintah perintah SPSS
dan baik file input data format baku tetap dengan tipe record tunggal, atau
sebuah ‘getfile’ dari data yang disimpan oleh dijalankan sebelumnya. Untuk
menghemat waktu berharga komputer yang dijalankan ‘edit’ yang bisa dilakukan
untuk memeriksa sintaks perintah tanpa menganalisis data. Dari versi 10
(SPSS-X) pada tahun 1983, file data dapat mengandung beberapa jenis catatan.
SPSS versi 16.0 berjalan di bawah Windows, Mac OS 10.5 dan sebelumnya, dan
Linux. User interface grafis ditulis di Jawa. Mac OS disediakan
sebagai Universal biner, membuat sepenuhnya kompatibel dengan baik PowerPC dan
Intel Mac berbasis hardware.
Sebelum SPSS 16.0, berbagai versi SPSS yang tersedia untuk Windows, Mac OS X
dan Unix. Versi Windows telah diupdate lebih sering, dan memiliki lebih
banyak fitur, daripada versi untuk sistem operasi lain.
SPSS versi 13.0 untuk Mac OS X tidak kompatibel dengan komputer Macintosh
berbasis Intel, karena perangkat lunak emulasi Rosetta menyebabkan kesalahan
dalam perhitungan.SPSS 15.0 for Windows membutuhkan perbaikan terbaru
download untuk diinstal supaya kompatibel dengan Windows Vista.
Pengaya
AMOS (Analisis Struktur Moment) – add-on yang memungkinkan pemodelan persamaan
struktural dan struktur kovarians, analisis jalur, dan memiliki kemampuan yang
lebih mendasar seperti analisis regresi linier, ANOVA dan ANCOVA
Release sejarah
SPSS 15.0.1 – November 2006
SPSS 16.0.2 – April 2008
Statistik SPSS 17.0.1 – Desember 2008
Statistik PASW 17.0.3 – September 2009
Statistik PASW 18,0 – Agustus 2009
Statistik PASW 18.0.1 – Desember 2009
Statistik PASW 18.0.2 – 2010 April
Pesaing
SAS (perangkat lunak)
Stata
Lihat juga
Daftar paket statistik
Perbandingan paket statistik
PSPP – pengganti bebas untuk SPSS
gretl – alternatif open source untuk SPSS yang dapat mengimpor data SPSS file
R Komandan – open source R-alternatif untuk SPSS
Catatan
^ Verlen Jason. “Penamaan Produk Panduan”. SPSS. Diperoleh
2009/09/18.
^ Press release
^ “Norman Nie”. Stanford University Jurusan Ilmu Politik. Diperoleh
2008/03/22.
^ Wellman, Barry “Melakukan itu sendiri”, Pp 71-78 di disyaratkan Reading: Buku
Paling Berpengaruh Sosiologi’s. Diedit oleh Clawson Dan, University of
Massachusetts Press, 1998, ISBN 9781558491533
Referensi
Argyrous, Statistik G. atau Penelitian: Dengan Panduan untuk SPSS, SAGE,
London, ISBN 1412919487
Levesque, Pemrograman R. SPSS dan Manajemen Data: Panduan bagi Pengguna SPSS
dan SAS, Edisi Keempat (2007), SPSS Inc, Chicago Illinois PDF ISBN 1568273908
SPSS 15.0 Command Reference Sintaks 2006, SPSS Inc, Chicago Illinois
Pranala luar
Situs resmi – dukungan halaman berisi database dicari solusi
Raynald Levesque’s SPSS Tools – perpustakaan solusi bekerja untuk programmer
SPSS (FAQ, sintaks perintah; macro, script, python)
Arsip SPSSX-L Diskusi – SPSS listserv aktif sejak tahun 1996.Membahas
pemrograman, statistik dan analisis
UCLA ATS Sumber Daya untuk membantu Anda mempelajari SPSS – Sumber untuk
belajar SPSS
UCLA ATS Teknis Laporan – Laporan 1 membandingkan Stata, SAS dan SPSS terhadap
R (R adalah bahasa dan lingkungan untuk komputasi statistik dan grafik).
Menggunakan SPSS Untuk Analisis Data – SPSS Tutorial dari Harvard
SPSS Pengembang Tengah – Dukungan untuk pengembang aplikasi yang menggunakan
SPSS, termasuk bahan dan contoh fitur programabilitas Python
JENIS DATA
Data adalah
kumpulan informasi yang diperoleh dari suatu pengamatan, dapat berupa
angka, lambang atau sifat. Menurut Webster New World Dictionary, pengertian
data adalah things known or assumed, yang berarti bahwa data
itu sesuatu yang diketahui atau dianggap. Diketahui artinya yang sudah terjadi
merupakan fakta (bukti). Data dapat memberikan gambaran tentang suatu keadaan
atau persoalan. Data bisa juga didefinisikan sebagai sekumpulan informasi atau
nilai yang diperoleh dari pengamatan (obsevasi) suatu objek. Data yang baik
adalah data yang bisa dipercaya kebenarannya (reliable), tepat waktu
dan mencakup ruang lingkup yang luas atau bisa memberikan gambaran tentang
suatu masalah secara menyeluruh merupakan data relevan.
dapat dibagi berdasarkan sifatnya, sumbernya, cara memperolehnya, dan
waktu pengumpulannya. Menurut sifatnya, jenis-jenis data yaitu:
Data
Kualitatif: data kualitatif adalah data yang tidak berbentuk angka,
misalnya: Kuesioner Pertanyaan tentang suasana kerja, kualitas pelayanan sebuah
rumah sakit atau gaya kepemimpinan, dll.
Data
Kuantitatif: data kuantitatif adalah data yang berbentuk angka, misalnya:
harga saham, besarnya pendapatan, dll.
Jenis-jenis
data menurut sumbernya, antara lain:
Data
Internal: data intenal adalah data dari dalam suatu organisasi yang
menggambarkan keadaan organisasi tersebut. Contohnya: suatu perusahaan, jumlah
karyawannya, jumlah modalnya, atau jumlah produksinya, dll.
Data
Eksternal: data eksternal adalah data dari luar suatu organisasi yang
dapat menggambarkan faktor-faktor yang mungkin mempengaruhi hasil kerja suatu
organisasi. Misalnya: daya beli masyarakat mempengaruhi hasil penjualan suatu
perusahaan.
Jenis-jenis
data menurut cara memperolehnya, antara lain:
Data Primer (primary
data): data primer adalah data yang dikumpulkan sendiri oleh
perorangan/suatu organisasi secara langsung dari objek yang diteliti dan untuk
kepentingan studi yang bersangkutan yang dapat berupa interview, observasi.
Data Sekunder
(secondary data): data sekunder adalah data yang diperoleh/ dikumpulkan
dan disatukan oleh studi-studi sebelumnya atau yang diterbitkan oleh berbagai
instansi lain. Biasanya sumber tidak langsung berupa data dokumentasi dan
arsip-arsip resmi.
Jenis-jenis
data menurut waktu pengumpulannya, antara lain:
Data cross
section, yaitu data yang dikumpulkan pada suatu waktu tertentu (at a point
of time) untuk menggambarkan keadaan dan kegiatan pada waktu tersebut.
Misalnya; data penelitian yang menggunakan kuesioner.
Data berkala (time
series data), yaitu data yang dikumpulkan dari waktu ke waktu untuk
melihat perkembangan suatu kejadian/kegiatan selama periode tersebut. Misalnya,
perkembangan uang beredar, harga 9 macam bahan pokok penduduk.
MEMBANGUN DATA
Langkah 1
Aktifkan
program Microsoft Excel hingga terdapat worksheet kosong.

Langkah 2
Klik FileMicrosoft
Excel yang berada di ujung kiri atas jendela utama. Klik Menu Options .

Langkah 3
di kotak dialog Excel
Options klik menu add-ins yang ada di jendela sebelah kiri.Pilih dan
Klik Analysis tool pack pada daftar aplikasi add-ins yang tidak aktif. Kemudian
Klik tombol Go, dan sebuah kotak dialog add-ins ditampilkan.

Langkah 4
Berikan tanda check
(lihat gambar) pada kotak check analysis tool pack.Kemudian klik tombol
OK dan tunggu beberapa saat sampai proses instalasi berakhir.

Langkah 5
Cara melakukan
analysis stastik deskriptif dengan Excel bisa dilakukan dengan beberapa langkah
yang sebenarnya siapa saja bisa melakukannya. Beberapa langkah yang dapat
dilakukan dalam standar proses analysis adalah sebagai berikut :
- Dari menu Data kemudian pilih Data Analysis

Analysis statistik
yang akan di lakukan adalah mencari ukuran pemusatan dari segugus data yang
diolah. Ukuran pemusatan merupakan sembarang ukuran yang menunjukkan pusat
segugus data yang telah diurutkan, dari yang terkecil sampai yang terbesar.
Ukuran pemusatan yang paling banyak antara lain :
- Mean.
Mean merupakan nilai
rata-rata atau nilai tengah dari segugus data.
- Median.
Median merupakan
nilai yang berada di tengah dari segugus data setelah diurutkan.
- Modus.
Modus merupakan nilai
yang paling sering muncul dari segugus data yang ada.
Contoh :
Hitung nilai mean, median, modus dari segugus data nilai Ujian Akhir
Semester, yaitu: 95, 75, 70, 80, 75, 68, 80, 78, 97, 85, 64, 100, 70, 67,
90, 68, 65, 89, dan 75.
Langkah 6
Input data seperti
contoh di bawah ini :

Langkah 7
Klik
menu Data pada menu Utama MS.Excel , dan klik menuData
Analysisyang ada di grup Analysis.

Langkah 8
- Pada kotak Dialog Analysis , pilih menu Descriptive Statistik, dan klik tombol OK untuk keluar dari kotak dialog tersebut.
- Klik button pada Input Range, dan masukkan data kedalam kolom Input Range, yaitu dengan cara mem-blok data pada sheet,
- Berikan tanda cek pada Label in First Row jika cell yang dimasukkan tadi memuat label dari data.
- Klik Output Range, klik pada kolom output range, dan tempatkan pointer pada sembarang cell yang kosong.
- pilihan Summary Statistics. Klik tombol OK.


Dan Ini lah
hasilnya :

INPUT DATA PADA
WORKSHEET
Input(memasukkan)
data secara manual pada cell worksheet Microsoft Excel. Kita dapat
memasukkan angka(baik angka utuh maupun desimal), teks, tanggal maupun waktu(jam)dalam satu cell.
Kita
juga bisa memasukkan data pada beberapa cell sekaligus. Sebuah file Microsoft Excel
adalah merupakan Workbook. Jika kita ibaratkan dia adalah sebuah buku. Dalam
Workbook terdiri dari worksheet(lembar kerja) atau spreadsheet. Worksheet bisa
kita ibaratkan lembaran-lembaran atau halaman-halaman dalam sebuah buku.Dalam
sebuah worksheet, terdiri dari cell cell yang diatur dalam kolom dan baris.
Pada cell cell itulah kita memasukkan(input) data. Memasukkan(input) angka
atau teks
- Pada worksheet,klik sebuah cell
- Tuliskan angka atau teks yang mau diinput. Kemudian tekan Enter atau Tab.
- Kalau kita ingin ganti baris tapi tetap dalam cell yang sama, sehabis input data tekannya Alt+Enter.
Note
:
- Pada settingan awal di Microsoft Excel, dengan tekan Enter, maka akan berpindah ke cell dibawahnya. Sedangkan dengan tekan Tab setelah input data, maka pilihan cell akan berpindah kekanan. Sehingga kita bisa menyesuaikan tekan Enter atau Tab.
- Pada saat kita menginput data dalam format angka,ada kemungkinan akan terlihat seperti ini ###### . Maka kita tinggal memperlebar kolom supaya angka terlihat semua.
- Untuk input angka yang tidak dimanfaatkan dalam perhitungan Excel(perhitungan matematika) contohnya No telepon(No Hp) kita bisa format kedalam format teks(text) saja. Contoh cara mengganti format cell untuk No Hp silahkan klik disini
Memasukkan(input)
data yang sama dalam beberapa cell sekaligus.
Kita bisa input data dalam beberapa cell atau range cell sekaligus dalam satu
waktu jika data yang kita masukkan sama. Berikut ini cara memasukkan data yang
sama dalam waktu bersamaan :
Pilih cell, range cell yang akan kita isi dengan data yang sama.
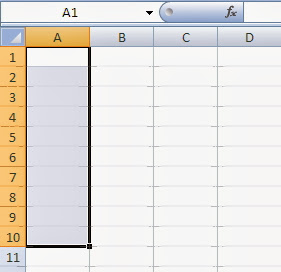
Dari
gambar di atas, kita akan memasukkan data yag sama pada cell A1 sampai A10
maka kita pilih A1 sampai A10
MENYIMPAN
DAN MEMBUKA DATA
Tutorial
ini bertujuan untuk:
- Menunjukkan langkah-langkah untuk memanggil SPSS
- Memberikan tuntunan proses memasukkan data ke dalam SPSS
Dalam tutorial ini dipergunakan IBM SPSS versi 22.
Memanggil
SPSS
Ketika
IBM SPSS 22 terbuka pertama kali Anda akan melihat kotak dialog di bawah ini.
Kotak dialog ini berfungsi menentukan kompatibilitas data yang disimpan dalam
file SPSS anda. Pilih Use Unicode encoding.
Dialog
box kompatibilitas encoding IBM SPSS 22
Ketika SPSS mulai bekerja, anda akan menjumpai jendela Data
Editor yang nampak pada gambar berikut. (Catatan: Anda mungkin perlu
menekan tombol Cancel pada kotak dialog yang muncul setelah kotak
dialog Unicode Mode untuk melihat jendela Data Editor).
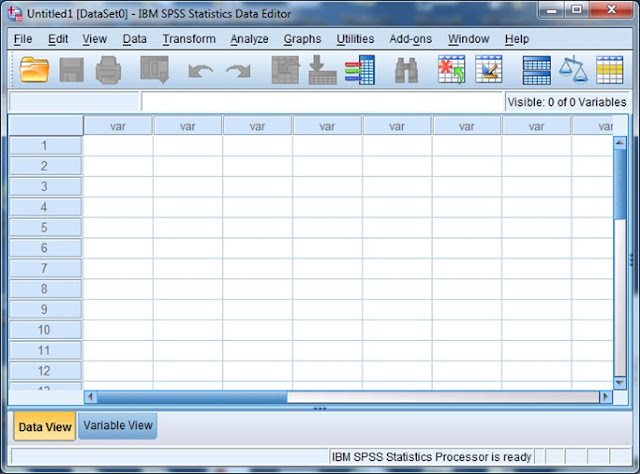
Tampilan
jendela Data Editor pada IBM SPSS
Memasukkan
atau membuka data pada SPSS
Untuk
memasukkan atau membuka data pada SPSS anda dapat:
- Mengetik langsung pada jendela Data Editor, atau
- Membuka file data SPSS yang telah ada sebelumnya, atau
- Melakukan operasi copy dan paste data dari software spreadsheet lainnya, misalnya Microsoft Excel.
Sebagai
contoh kita akan mencoba membuka data BellaireGraduates.sav (unduh terlebih dahulu file
ini). Membuka file data SPSS yang telah tersimpan dalam hard disk dapat
dilakukan dengan menekan menu File
> Open > Data dari menu drop-down (atau
pilih Open an Existing Data Source ketika SPSS meminta Anda untuk
menentukan What would you like to do?). Anda kemudian akan menjumpai
dialogue box yang nampak pada gambar berikut.
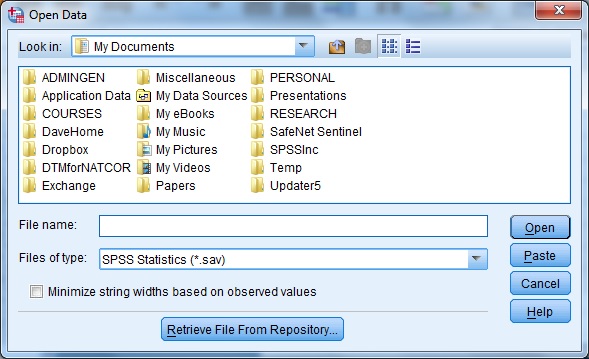
Dialogue
box pada menu open data
Anda kemudian perlu mencari folder yang menyimpan file data
BellaireGraduates.sav, memilih file ini, kemudian menekan tombol Open.
Setelah itu Anda akan menjumpai jendela yang ditunjukkan berikut ini.
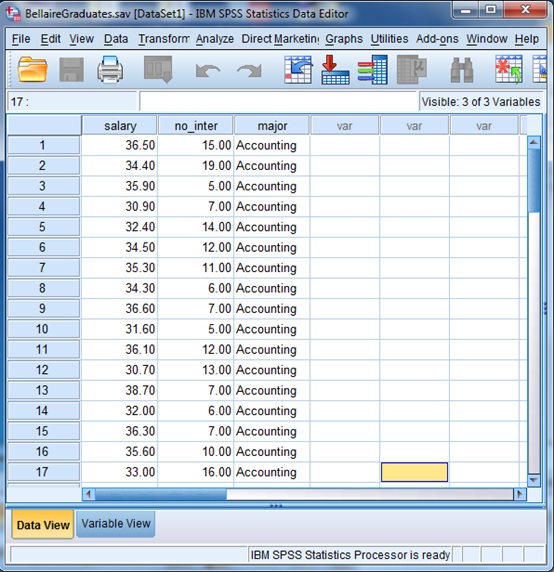
Tampilan
data dalam file BellaireGraduates
File
data ini menunjukkan gaji awal (dalam $’000) dari sebuah sampel yang terdiri
atas 50 orang lulusan universitas di Amerika, jumlah wawancara kerja yang
pernah mereka lalui dan bidang studi mereka (Accounting, Information Systems
dan Marketing). Gaji (variabel ‘Salary’) dan jumlah wawancara kerja (variabel
‘no. of interviews’) merupakan variabel-variabel kuantitatif, sementara bidang
studi (variabel ‘major’) merupakan variabel yang bersifat kualitatif.
MEMODIFIKASI
DATA
Memodifikasi
referensi data bagan
Anda
dapat memodifikasi referensi data bagan di editor data bagan. Anda hanya dapat
memasukkan angka, tanggal, atau durasi di sel data.
Menambahkan,
menghapus, atau mengedit deretan data
- Pilih bagan, klik Edit Data Bagan, lalu lakukan salah satu hal berikut:
- Menambahkan deretan data: Klik sel di kolom atau baris baru, lalu masukkan data Anda.
- Menghapus deretan data: Klik bar berwarna untuk baris atau kolom yang ingin Anda hapus, klik panah yang muncul, lalu klik Hapus Kolom atau Hapus Baris (tergantung apakah Anda merancang baris atau kolom sebagai deretan data).
- Mengurutkan ulang deretan data: Seret bar berwarna untuk mengurutkan ulang deretan data bagan.
- Menambahkan simbol mata uang atau pemformatan lain: Klik tab Deretan di bagian atas bar samping di sebelah kanan, lalu gunakan kontrol di tab Deretan.
- Mengedit label nilai dan format angka: Klik tab Deretan pada bagian atas bar samping di sebelah kanan, klik segitiga pengungkapan di samping Label Nilai, lalu pilih kotak centang Nilai. Klik menu pop-up untuk memilih sumbu yang diinginkan, lalu gunakan kontrol di bagian Format Data Nilai untuk membuat pengaturan.
2. Tutup
jendela Data Bagan untuk kembali ke bagan.
Mengubah
baris dan kolom menjadi deretan data
Jika
Anda menambahkan bagan, Keynote menetapkan default deretan data untuknya. Dalam sebagian
besar kasus, jika tabel berbentuk persegi atau lebih lebar dari tingginya,
baris tabel adalah deretan defaultnya. Jika tidak, kolom adalah deretan
defaultnya. Anda dapat mengubah apakah baris atau kolom merupakan deretan data.
- Pilih bagan, lalu klik Edit Data Bagan.
- Klik baris atau kolom di pojok kanan atas editor Data Bagan.

3. Tutup
jendela Data Bagan jika sudah selesai.
Membagikan
sumbu-x untuk beberapa nilai di sepanjang sumbu-y untuk bagan sebar dan
gelembung
Membagikan
sumbu-x berarti menyusun satu jenis nilai di sepanjang sumbu-x, sambil mengizinkan
beberapa jenis nilai dirancang di sepanjang sumbu-y. Secara default, nilai
sumbu x dibagikan di antara beberapa kumpulan nilai sumbu y pada beberapa jenis
bagan.

- Pilih bagan, lalu klik Edit Data Bagan.
- Klik
 , lalu
pilih (atau batal pilih) Bagikan Nilai X.
, lalu
pilih (atau batal pilih) Bagikan Nilai X. - Tutup jendela Data Bagan jika sudah selesai.
MENGIMPOR
DATA KE SPSS
Setelah
kita menginput data di MS Excel (lihat: Entry
data 1),
selanjutnya akan kita bahas bagaimana cara mengekspor data yang telah kita
input tersebut ke SPSS.
Misalkan data yang sudah kita input di MS Excel adalah:
|
No
|
Tingkat
Pendidikan
|
JK
|
Tinggi
|
Berat
|
Soal1
|
|
1
|
1
|
1
|
166
|
70
|
4
|
|
2
|
2
|
2
|
157
|
45
|
3
|
|
3
|
3
|
1
|
156
|
77
|
3
|
|
4
|
1
|
1
|
160
|
50
|
1
|
|
5
|
1
|
1
|
160
|
50
|
1
|
|
6
|
1
|
1
|
170
|
54
|
2
|
|
7
|
1
|
1
|
164
|
50
|
4
|
|
8
|
2
|
2
|
190
|
90
|
4
|
|
9
|
2
|
2
|
154
|
67
|
4
|
|
10
|
2
|
2
|
163
|
78
|
1
|
|
11
|
1
|
1
|
155
|
52
|
1
|
|
12
|
2
|
2
|
158
|
55
|
2
|
|
13
|
1
|
1
|
164
|
56
|
4
|
|
14
|
3
|
1
|
174
|
66
|
4
|
|
15
|
1
|
1
|
156
|
60
|
2
|
|
16
|
1
|
1
|
170
|
56
|
3
|
|
17
|
3
|
2
|
161
|
64
|
4
|
|
18
|
2
|
1
|
178
|
67
|
2
|
Selanjutnya
ikuti langkah-langkah berikut ini:
LANGKAH 1:
Buka SPSS
(eh ya, untuk dipenjelasan ini, saya menggunakan SPSS versi 16, mengingat itu
yang ada di laptop, hehehe. Walaubagaimanapun versi apapun yang kita pakai,
hitung-hitungan statistiknya sama saja, paling fitur-fiturnya saja yang
berbeda)
LANGKAH 2:
Klik File à Open à Data… à Ubah
Files of Type menjadi Excel à cari data Excel tempat data kita
tersimpan à Open à Klik Variable Names from the first
row of data à Pilih sheet tempat kita berada à Continue
LANGKAH 3:
Klik Variable
View à delete baris No (karena ini tidak perlu) à Pada
lajur Column semuanya ubah menjadi 8 biar lebar sheetnya
lebih proposional à Pada lajur Measure ubah label sesuai dengan
jenis data.
Keterangan
|
Jenis data
|
Ciri
|
Contoh
|
|
Nominal
|
Hanya sebagai
label, tidak bisa dilakukan perhitungan aritmatika, data bersifat setara
|
merk motor, jenis
kelamin, pekerjaan, dll
|
|
Ordinal
|
Sama dengan nominal
(sebagai label, tidak bisa dilakukan perhitungan aritmatika), bedanya data
bersifat bertingkat
|
jenjang pendidikan,
tingkat kepedasan, tingkat kepuasan, dll
|
|
Scale
|
yang bisa dilakukan
perhitungan aritmatika
|
berat, tinggi,
jumlah saudara, harga barang, dll
|
LANGKAH 4:
Selanjutnya perlu
kita defenisikan untuk setiap jenis data nominal dan ordinal. Penjelasannya ada
dipostingan selanjutnya :D
Catatan: Selain cara
di atas, mentransfer data dari Excel ke SPSS, bisa dilakukan dengan
mengcopy langsung dari file MS Excel dan di paste ke SPSS, hanya saja pada
lajur Name, mesti kita tulis lagi secara manual.
MENU PADA SPSS
Sebagaimana program
lainnya, SPSS juga memiliki berbagai menu untuk melakukan perintah yang
diberikan. Menu-menu utama pada SPSS adalah sebagai berikut:

File : menu dasar untuk membuka, menyimpan serta melakukan pengolahan
file.
Edit : untuk memperbaiki dan mengolah data yang telah dimasukkan
View : untuk mengatur tampilan menu dalam SPSS
Data : untuk melakukan pengaturan terhadap data yang telah dimasukkan
sebelum dilakukan proses analisis.
Trasform : untuk melakukan transformasi data sebelum dilakukan analisis
Analyze : menu yang paling penting dalam SPSS, untuk melakukan berbagai
macam analisis statistik di SPSS.
Direct Marketing : menu terbaru SPSS untuk melakukan analisis marketing
Graphs : menu untuk membuat berbagai macam grafik.
Add-Ons : menu untuk menambah program tambahan yang berkaitan dengan SPSS
Window : menu untuk mengatur tampilan jendela
Help : Menu bantuan apabila mengalamai kesulitan dalam menggunakan SPSS.
Di dalam menu Help terdapat Tutorial SPSS. Anda dapat belajar lebih banyak
di menu ini.

BUILDING CHARTS
1. Grafik batang
Grafik batang adalah
grafik yang penyajian datanya mengunakan batang atau persegi panjang.
Grafik batang atau sering kita kenal dengan sebutan histogram. Grafik batang
dipakai untuk memperlihatkan perbedaan tingkat nilai dari beberapa aspek
pada suatu data. Grafik batang merupakan grafik yang paling sederhana diantara
jenis-jenis grafik lainnya. Karena grafik ini sangat mudah untuk dipahami dan
hanya menggambarkan data dalam bentuk batang.

Panjang batang
merupakan gambaran dari presentase data, sedangkan lebar batang tidak
berpengaruh apa-apa. Namun, pada umumnya data yang dapat kita bandingkan dengan
grafik ini tidak bisa banyak, maksimal data yang dapat kita bandingkan hanya
delapan data. Untuk dapat memperjelas perbandingan antara data satu
dengan yang lain maka setiap batang harus memiliki warna-warna yang berbeda.
2. Grafik Garis
Grafik garis adalah
grafik yang penyajian datanya mengunakan garis atau kurva. Grafik garis banyak
digunakan untuk menggambarkan suatu perkembangan atau perubahan dari waktu ke
waktu pada sebuah objek yang di teliti. Garfik ini terdiri dari 2 sumbu utama
yakni sumbu X dan sumbu Y. Untuk pengunaaanya sumbu X biasanya digunakan untuk
menunjukkan waktu pengamatan. Sedangkan sumbu Y digunakan untuk menunjukkan
nilai hasil pengamatan pada waktu-waktu tertentu. Waktu dan hasil
pengamatan dikumpulkan dengan titik-titik pada bidang XY.

Kemudian dari
tiap-tiap titik yang berdekatan dihubungkan dengan garis sehingga akan
menghasilkan garfik garis atau sering disebut juga diagram garis. Misalnya,
kita akan membuat garfik garis dari data pengunjung situs facebook dari
hari senin sampai sabtu. Pada sumbu x kita dapat menulisakan tahun mulai dari
senin sampai sabtu dan pada sumbu y kita dapat menuliskan angka atau nilai
hasil yang diperoleh. Biasanya angka tersebut berupa sekala mulai dari 0 sampai
angka hasil tertinggi yang diperoleh dalam penelitian. Contoh : 0,50, 100, 150,
200, dst.
3. Grafik lingkaran
Grafik lingkaran
adalah grafik yang penyajian datanya mengunakan lingkaran. grafik lingkaran
merupakan gambaran naik turunnya data yang berupa lingkaran untuk menggambarkan
persentase dari nilai total suatu data. Dalam membuat grafik lingkaran ada
beberapa hal yang harus kita perhatikan yakni, kita tentukan terlebih dahulu
besar persentase tiap objek terhadap keseluruhan data dan kemudian kita
tentukan besarnya sudut masing-masing kelompok data. Untuk menetukan presentase
suatu kelompok data dapat kita laukan dengan cara jumlah suatu kelompok data di
bagi dengan jumlah total seluruh data di kali 100%.

Dan untuk menentukan
besar sudutnya dapat kita lakukan dengan cara membagi hasil presentase kelompok
data dengan 360. Yang kedua kita tentukan warna masing-masing kelompok
data. Warna tersebut digunakan untuk mebedakan antara kelompok data satu dan
lainnya. Misalnya, kita akan membuat diagram lingkaran dari data Pengasilan
masyarakat desa Karangdoro. Macam-macam penghasilan yang kita peroleh kita
kelompokkan berdasarkan jenisnya. Lalu kita tentukan presentase, besar sudut
dan warna dari masing-masing hobi dengan cara seperti yang sudah di jelaskan.
PENGUKURAN DESKRIPTIF
Deskripsi adalah pemaparan atau penggambaran dengan kata-kata secara jelas dan
terperinci (KBBI, 2001:258). Sedangkan statistik deskriptif merupakan alat
analisis untuk menjelaskan, meringkas, mereduksi, menyederhanakan,
mengorganisasi dan menyajikan data ke dalam bentuk yang teratur, sehingga mudah
dibaca, dipahami dan disimpulkan (Wiyono, 2001). Statistik deskriptif digunakan
untuk mendeskripsikan suatu keadaan atau masalah agar lebih mudah dipahami.
Analisis deskriptif
merupakan analisis yang paling mendasar untuk menggambarkan keadaan data secara
umum. Analisis deskriptif ini meliputi beberapa hal, yakni distribusi
frekuensi, pengukuran tendensi pusat, dan pengukuran variabilitas (Wiyono,
2001)
4. Distribusi frekuensi.
Distribusi frekuensi merupakan susunan data-data mentah yang acak dan sulit
dibaca yang kemudian disusun berdasarkan kategori tertentu dalam suatu daftar
secara sistematis agar mudah dipahami. Distribusi frekuensi dibagi menjadi
beberapa jenis yaitu distribusi frekuensi secara tidak berkelompok, distribusi
rank order, distribusi frekuensi secara berkelompok, dan grafik distribusi.
5. Pengukuran Tendensi
Pusat. Ukuran tendensi pusat merupakan suatu ukuran yang merupakan wakil
kumpulan data untuk mendapatkan gambaran yang lebih jelas mengenai data
tersebut baik mengenai sampel ataupun populasi. Beberapa macam ukuran tendensi
sentral yaitu rata-rata (mean), median dan modus. Tendensi pusat digunakan
untuk melihat letak bagian terbesar dalam distribusi.
6. Pengukuran
Variabilitas. Pengukuran variabilitas untuk menggambarkan derajat berpencarnya
data kuantitatif. Ukuran ini terdiri atas rentang antarkuartil, simpangan
kuartil, rata-rata simpangan, simpangan baku dan koefisien variasi, serta
varian. Pengukuran variabilitas berfungsi untuk mengetahui homogenitas atau
heterogenitas data. Suatu data bisa saja memiliki nilai tendensi pusat yang
sama namun memiliki nilai variansi yang berbeda
Dalam analisis
deskriptif, data-data disajikan dalam bentuk tabel, diagram, grafik, dan
lain-lain. Hal ini ditujukan untuk mempermudah memahami data-data yang
disajikan. Dalam ilmu perencanaan, penggunaan statistik deskriptif dapat
dilakukan untuk mempermudah penyampaian informasi agar mudah diterima dan
dipahami.
Analisis deskriptif
terdiri dari mean, median, modus, simpangan baku dan varian. Terdapat empat
data yang digunakan yaitu data nominal, data ordinal, data interval dan data
rasio. Namun, terdapat batasan dalam penggunaan data dengan skala-skala
tertentu. Data nominal hanya dapat digunakan untuk mengetahui modus karena data
nominal merupakan data yang paling sederhana. Data ordinal dapat digunakan
untuk mengetahui modus dan median. Sedangkan data interval dan rasio digunakan
untuk mengetahui baik modus, median, mean maupun simpangan baku. Hal ini
dikarenakan untuk menghitung mean hanya dapat dilakukan dengan menggunakan data
yang bisa dilakukan operasi matematik seperti tambah, kurang, kali, bagi dan
lain-lain.
Dalam analisis
deskriptif, terdapat dua cara yaitu secara manual dan menggunakan software
SPSS. Untuk cara manual, dapat digunakan rumus-rumus matematis sebagai berikut.
- Rata-rata (Mean)
Rumus data
tunggal:
Rumus
data berkelompok: 

- Modus
Untuk data tunggal,
nilai yang paling banyak jumlahnya merupakan modus. Misalnya dari data x1, x2,
x3…. xn, xi adalah yang paling banyak muncul, maka xi adalah modus. Dengan kata
lain, modus adalah frekuensi yang paling banyak.
Rumus data berkelompok:

- Median
Untuk data tunggal,
median terletak pada pertengahan data yang sudah diurutkan. Data yang berjumlah
ganjil, maka nilai tengah dapat langsung ditentukan. Namun, untuk data yang
berjumlah genap, nilai median adalah rata-rata dari dua datum yang berada di
pertengahan.
Rumus data berkelompok:

- Simpangan baku dan varian
Rumus data
tunggal: Rumus data berkelompok:


Contoh Kasus
Pembangunan berkelanjutan merupakan proses pembangunan yang secara
berkelanjutan mengoptimalkan manfaat dari sumber daya alam dan manusia dengan
menyeimbangkan antara aktivitas manusia dan kemampuan alam. Dengan kata lain,
pembangunan berlangsung secara berlanjut dan didukung oleh sumber alam dengan kualitas
lingkungan dan manusia semakin berkembang. Pembangunan berkelanjutan dalam
kaitannya dengan kependudukan terlihat pada ketersediaan sumber daya alam yang
nantinya dikonsumsi oleh manusia.
Jumlah penduduk yang
tidak terkendali dalam jangka waktu yang panjang akan menimbulkan dampak
kelangkaan sumber daya alam sebagai isu utama dalam perekonomian. Sumber alam
terutama udara, air dan tanah, memiliki ambang batas dimana pemanfaatan yang
berlebihan akan menyebabkan berkurangnya kuantitas dan kualitas sumberdaya alam
sehingga mengurangi kemampuannya mendukung kehidupan umat manusia. Penggunaan
bahan baku dari alam seperti kayu, bahan pangan, logam yang digunakan dalam
perindustrian akan meningkat seiring dengan peningkatan kebutuhan penduduk.
Oleh karena itu dibutuhkan upaya pengendalian jumlah penduduk agar alam mampu
mendukung kehidupan manusia hingga masa yang akan datang.
Untuk mengatasi
masalah kependudukan, pemerintah mencanangkan program Keluarga Berencana di
seluruh penjuru Indonesia. Namun, keberhasilan dari program ini juga sangat
dipengaruhi oleh persepsi atau pemikiran masyarakat itu sendiri terutama bagi
warga masyarakat yang berlatarbelakang ilmu pengetahuan dan pendidikan yang
rendah, sehingga diperlukan sosialisasi atau penyuluhan mengenai program
tersebut agar masyarakat dapat membuka pikiran.
Kota Surabaya
merupakan salah satu kota metropolitan di Indonesia dengan jumlah penduduk
lebih dari 1 juta jiwa. Pada sensus tahun 2010, jumlah penduduk Kota Surabaya
tercatat sebanyak 2.765.908 jiwa yang tersebar di 31 kecamatan. Untuk
menanggapi isu kelangkaan sumber daya alam dalam rangka pembangunan
berkelanjutan di Kota Surabaya, dapat dilakukan dengan melihat kecenderungan
pemerataan jumlah penduduk pada seluruh kecamatan. Selain itu, dapat dilakukan
penyuluhan program Keluarga Berencana sebagai upaya penekanan jumlah penduduk.
Dalam melakukan hal tersebut perlu diperhatikan lokasi yang paling membutuhkan
sosialisasi program Keluarga Berencana dengan mempertimbangkan rata-rata jumlah
anggota rumah tangga dan kepadatan penduduk di suatu Kecamatan.
Analisis deskriptif
ini bertujuan untuk menentukan daerah yang diutamakan dalam pengendalian jumlah
penduduk yang dilakukan dengan penyuluhan mengenai program Keluarga Berencana.
Data yang digunakan dalam analisis ini adalah data dalam bentuk nominal dan
scale dengan tipe data string dan Numeric. Ketentuannya adalah dimana suatu
daerah memiliki tingkat kepadatan penduduk serta rata-rata jumlah anggota rumah
tangga yang tinggi. Berikut kategori pada kepadatan penduduk dan rata-rata
jumlah anggota rumah tangga.
|
Kepadatan Penduduk:
– 5000 : Rendah – 5001-15000 : Sedang – 15001 :Tinggi |
Rata-rata jumlah
anggota rumah tangga:
– 3,50 : Rendah – 3,51 : Tinggi |
Berikut tabel data
jumlah penduduk, jumlah rumah tangga serta luas wilayah.
Tabel Jumlah
Penduduk, Jumlah Rumat Tangga dan Luas Wilayah Kota Surabaya Per Kecamatan pada
Tahun 2010

Output dan Analisis
Berikut hasil perhitungan menggunakan SPSS.
Tabel Hasil Perhitungan
dan Pengkategorian Rata-rata Anggota Rumah Tangga dan Kepadatan Penduduk
Tahun 2010

Nilai rata-rata
anggota rumah tangga diperoleh dari jumlah penduduk total yang dibagi dengan
jumlah rumah tangga menggunakan menu Transform à Compute
Variable pada SPSS. Sedangkan nilai kepadatan penduduk diperoleh dari
perbandingan jumlah penduduk dengan luas wilayah. Dari data di atas, dapat
diketahui bahwa di Kota Surabaya terdapat tujuh kecamatan yang lebih diutamakan
dalam pengendalian jumlah penduduk. Kecamatan tersebut yaitu:
- Bubutan
- Simokerto
- Semampir
- Kenjeran
- Tambaksari
- Mulyoreo
- Wonokromo
Ketujuh kecamatan
tersebut perlu mendapatkan perhatian karena rata-rata jumlah penduduknya yang
tinggi pada kepadatan penduduk yang tinggi pula yaitu memiliki nilai rata-rata
anggota rumah tangga lebih dari 3,51 dan nilai kepadatan penduduk yang lebih
dari 15.001 jiwa/km2 sehingga perlu diadakan sosialisasi atau penyuluhan
yang lebih gencar mengenai program Keluarga Berencana.
Berikut tabel hasil
perhitungan menggunakan metode Analyze à Descriptive
Statistics à Frequencies (tabel 3.2) dan
metode Analyze à Descriptive
Statistics à Descriptives.
Tabel Hasil
Perhitungan Frequencies

Pada tabel
Frequencies di atas diperoleh data Mean, Median, Mode, Standard Deviation,
Variance, Minimum, Maximum dan Sum. Menu Frequencies lebih lengkap jika
dibandingkan dengan menu Descriptives. Dari tabel di atas dapat diketahui:
- Kevalidan data, yaitu jumlah data yang diproses sama dengan jumlah data yang diinput yaitu 31 data.
- Nilai rata-rata untuk jumlah penduduk sebesar 89222.84, jumlah rumah tangga 24804.26, luas wilayah 10.5445, kepadatan penduduk 11300.57 dan rata-rata anggota rumah tangga 3.6227
- Nilai tengah untuk jumlah penduduk sebesar 79179.00, jumlah rumah tangga 22314.00, luas wilayah 8.7600, kepadatan penduduk 10222.35 dan rata-rata anggota rumah tangga 3.6963
- Modus untuk jumlah penduduk sebesar 37525a , jumlah rumah tangga 9544a, luas wilayah 9.23, kepadatan penduduk 2088a dan rata-rata anggota rumah tangga 2.86a
- Standard deviation untuk jumlah penduduk sebesar 42839.582, jumlah rumah tangga 11762.313, luas wilayah 6.11474, kepadatan penduduk 089 dan rata-rata anggota rumah tangga 0.28654
- Nilai varian untuk jumlah penduduk sebesar 1.835E9 , jumlah rumah tangga 1.384E8, luas wilayah 37.390, kepadatan penduduk 5.576E7 dan rata-rata anggota rumah tangga 0.082. Nilai E merupakan kelipatan 10.
- Nilai terendah untuk jumlah penduduk sebesar 37525, jumlah rumah tangga 9544, luas wilayah 2.59 , kepadatan penduduk 2088 dan rata-rata anggota rumah tangga 2.86.
- Nilai tertinggi untuk jumlah penduduk sebesar 205381, jumlah rumah tangga 55564, luas wilayah 23.72, kepadatan penduduk 30571 dan rata-rata anggota rumah tangga 4.02.
- Jumlah total untuk jumlah penduduk sebesar 2765908 , jumlah rumah tangga 768932, luas wilayah 326.88, kepadatan penduduk 350318 dan rata-rata anggota rumah tangga 112.30.
Pada Frequencies,
tabel frekuensi juga ditampilkan. Tabel frekuensi merupakan tabel yang
menunjukkan berapa kali suatu nilai muncul. Selain itu juga terdapat persentase
kemunculan tersebut, serta kumulatif dari persentase. Tabel frekuensi terlampir
beserta diagram pie.
Tabel Hasil
Perhitungan Descriptive

Pada dasarnya, muatan
pada kedua tabel di atas hampir sama. Terdapat Mean, Maximum, Minimum,
Simpangan Baku dan Varian. Namun menu yang terdapat pada Descriptives tidak
selengkap Frequencies dan tidak menunjukkan kevalidan data. Descriptives
menyajikan hasil analisis dalam satu tabel saja.
Kesimpulan
Berdasarkan hasil analisis yang dilakukan, dapat diambil kesimpulan bahwa:
- Semua data yang diinput adalah valid, artinya semua data diproses tanpa ada yang hilang yaitu sebanyak 31 data.
- Analisis deskriptif dapat dilakukan dengan menggunakan analisis frequencies dan analisis descriptive.
- Nilai rata-rata untuk jumlah penduduk sebesar 89222.84, jumlah rumah tangga 24804.26, luas wilayah 10.5445, kepadatan penduduk 11300.57 dan rata-rata anggota rumah tangga 3.6227
- Nilai tertinggi untuk jumlah penduduk sebesar 205381 pada Kecamatan Tambaksari , jumlah rumah tangga 55564 pada Kecamatan Tambaksari, luas wilayah 23.72 pada Kecamatan Benowo, kepadatan penduduk 30571 yang terdapat pada Kecamatan Simokerto dan rata-rata anggota rumah tangga 4.02 di Kecamatan Kenjeran.
- Suatu kecamatan dikatakan memiliki kepadatan penduduk yang tinggi apabila bernilai lebih dari atau sama dengan 15.001 jiwa/km2.
- Suatu kecamatan dikatakan memiliki rata-rata jumlah anggota rumah tangga yang tinggi apabila bernilai lebih dari atau sama dengan 3,51.
Daerah yang
diutamakan dalam pengendalian jumlah penduduk sebagai langkah dalam proses
pembangunan berkelanjutan yaitu daerah yang memiliki rata-rata jumlah anggota
rumah tangga dan kepadatan penduduk yang sama-sama tinggi
UJI NORMALITAS
Uji normalitas
digunakan untuk mengetahui data yang akan dianalisis berdistribusi normal atau
tidak. Secara fundamental, data yang berdistribusi normal dapat diketahui
melalui bentuk histogram seperti lonceng. Terdapat banyak uji normalitas untuk
mengetahui distribusi data.
A. Pengertian Uji Normalitas Shapiro WilK
Uji Normalitas Shapiro Wilk adalah uji yang dilakukan untuk mengetahui
sebaran data acak suatu sampel kecil. Dalam 2 seminar paper yang dilakukan
Shapiro, Wilk tahun 1958 dan Shapiro, Wilk, Chen 1968 digunakan simulasi data
yang tidak lebih dari 50 sampel. Sehingga disarankan untuk menggunakan uji
shapiro wilk untuk sampel data kurang dari 50 sampel (N<50). Dalam
pengujian, suatu data dikatakan berdisitribusi normal apabila nilai
signifikansi >0.05 (sig. >0.05).
B. Pengertian Uji
Normalitas Kolmogorov Smirnov
Uji Normalitas
Kolmogorov Smirnov adalah uji yang dilakukan untuk mengetahui sebaran data
acak dan spesifik pada suatu populasi (Chakravart, Laha, and Roy, 1967).
Berdasarkan pengujian yang dilakukan National Institute of Standars and
Technology, uji kolmogorov smirnov menghasilkan performa yang baik untuk ukuran
data 20-1000. Namun dalam penelitian pada umumnya, pengujian kolmogorov smirnov
masih digunakan untuk sampel data yang berukuran lebih dari 2000 sampel.
Sehingga disarankan untuk menggunakan uji kolmogorov smirnov untuk data diatas
50 sampel (20≤N≤1000). Dalam pengujian, suatu data dikatakan
berdisitribusi normal apabila nilai signifikansi >0.05 (sig. >0.05).
C. Cara Uji
Normalitas SPSS beserta Grafiknya
Contoh: Melakukan
Uji Normalitas keseluruhan data
Diketahui pada Data View berikut (menggunakan tampilan value labels)
berisi data nilai ujian matematika dari 20 siswa suatu kelas.
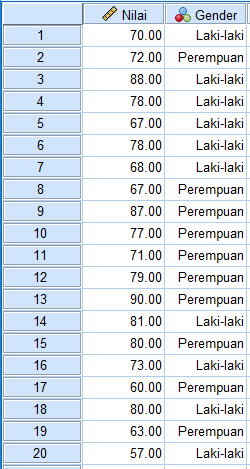
Dengan variabel pada data SPSS
Berikut langkah-langkah untuk melakukan uji normalitas pada SPSS,
1. Klik Analyze
> Descriptive Statistics > Explore…
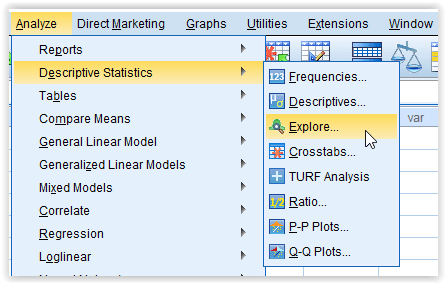
2. Masukkan variabel
yang dilakukan pengujian normalitas pada jendela Explore
Masukkan variabel
dilakukan pengujian ke kolom Dependent List. Kita juga dapat memasukkan
variabel ke Factor List untuk melakukan pengujian berdasarkan kriteria
tertentu, misalnya uji normalitas data yang dibedakan berdasarkan jenis
kelamin.
Catatan: Anda dapat memasukkan beberapa variabel sekaligus
di Dependent List untuk menguji normalitas masing-masing varibel,
misalnya uji normalitas 2 variabel atau 3 variabel.
3. Klik Plots.. pada
jendela Explore dan centang Normality plot with tests
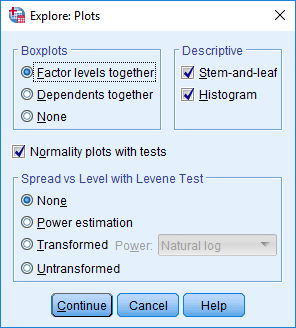
- Boxplots: Untuk membuat Boxplot data
- Descriptive: Untuk melakukan analisis deskriptif serta membuat grafik Steam-and-leaf atau Histogramnya (centang jika diperlukan)
- Normality plots with tests: untuk melakukan pengujian normalitas
4. Klik Continue lalu
klik OK
5. Hasil pengujian
ditampilkan pada jendela output
D. Membaca Hasil Uji
Normalitas SPSS
Untuk mempermudah
membaca hasil analisis anda dapat menggunakan panel navigasi pada jendela
ouput.
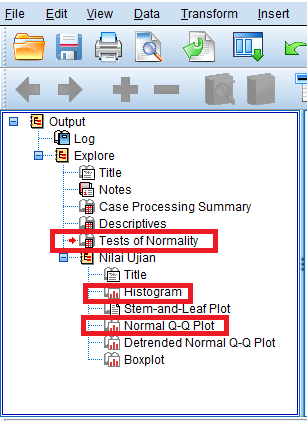
Hasil Pengujian
Normalitas (Test of Normality)
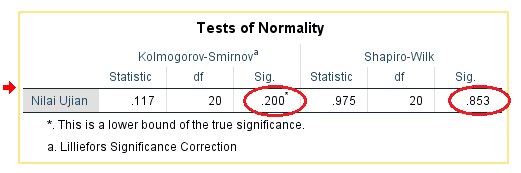
Nilai signifikansi
(p) pada uji kolmogorov-smirnov adalah 0.2 ( p > 0.05), sehingga berdasarkan
uji normalitas kolomogorov-smirnov data berdistribusi normal.
Nilai signifikansi (p) pada uji shapiro-wilk adalah 0.853 ( p > 0.05),
sehingga berdasarkan uji normalitas shapiro-wilk data berdistribusi normal.
Histogram Data
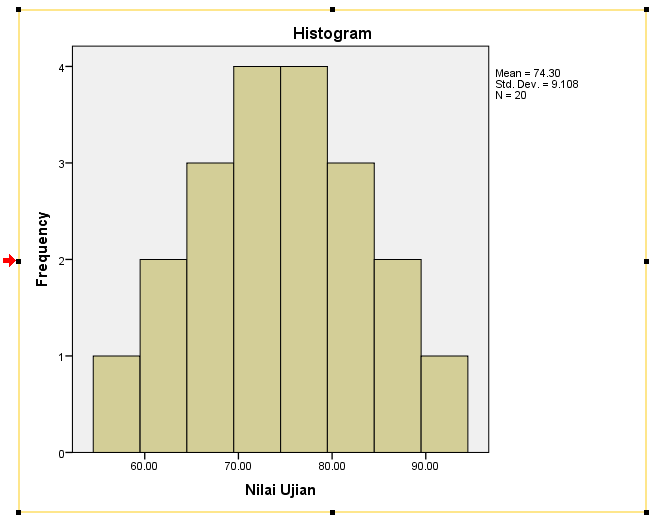
Terlihat bentuk
histogram data hampir menyerupai lonceng.
Normal Q-Q Plot
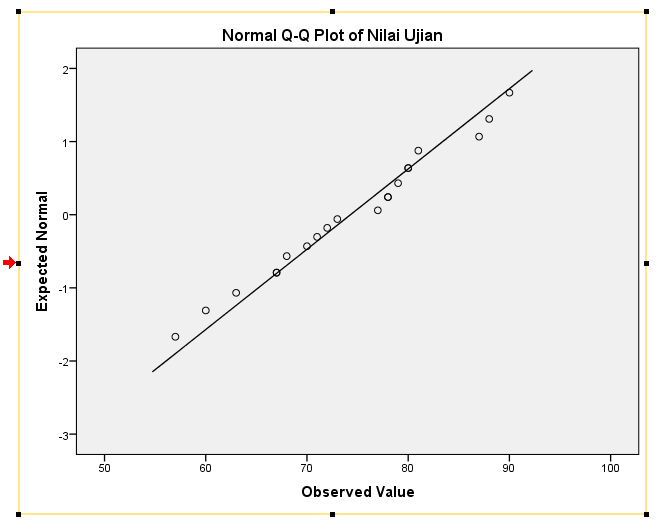
Q-Q Plot baik digunakan dengan data N≥20 untuk melihat keragaman sebaran data
univariat (1 variabel)
.
PENGERTIAN KORELASI
Secara sederhana,
korelasi dapat diartikan sebagai hubungan. Namun ketika dikembangkan lebih
jauh, korelasi tidak hanya dapat dipahami sebatas pengertian tersebut. Korelasi
merupakan salah satu teknik analisis dalam statistik yang digunakan untuk
mencari hubungan antara dua variabel yang bersifat kuantitatif. Hubungan dua
variabel tersebut dapat terjadi karena adanya hubungan sebab akibat atau dapat
pula terjadi karena kebetulan saja. Dua variabel dikatakan berkolerasi apabila
perubahan pada variabel yang satu akan diikuti perubahan pada variabel yang
lain secara teratur dengan arah yang sama (korelasi positif) atau berlawanan
(korelasi negatif).
Dalam Matematika,
korelasi merupakan ukuran dari seberapa dekat dua variabel berubah dalam
hubungan satu sama lain. Sebagai contoh, kita bisa menggunakan tinggi badan dan
usia siswa SD sebagai variabel dalam korelasi positif. Semakin tua usia siswa
SD, maka tinggi badannya pun menjadi semakin tinggi. Hubungan ini disebut
korelasi positif karena kedua variabel mengalami perubahan ke arah yang sama,
yakni dengan meningkatnya usia, maka tinggi badan pun ikut meningkat.
Sementara itu, kita
bisa menggunakan nilai dan tingkat ketidak hadiran siswa sebagai contoh dalam
korelasi negatif. Semakin tinggi tingkat ketidak hadiran siswa di kelas, maka
nilai yang diperolehnya cenderung semakin rendah. Hubungan ini disebut korelasi
negatif karena kedua variabel mengalami perubahan ke arah yang berlawanan,
yakni dengan meningkatnya tingkat ketidak hadiran, maka nilai siswa justru
menurun.
Kedua variabel yang
dibandingkan satu sama lain dalam korelasi dapat dibedakan menjadi variabel
independen dan variabel dependen. Sesuai dengan namanya, variabel independen
adalah variabel yang perubahannya cenderung di luar kendali manusia. Sementara
itu variabel dependen adalah variabel yang dapat berubah sebagai akibat dari
perubahan variabel indipenden. Hubungan ini dapat dicontohkan dengan ilustrasi
pertumbuhan tanaman dengan variabel sinar matahari dan tinggi tanaman. Sinar
matahari merupakan variabel independen karena intensitas cahaya yang dihasilkan
oleh matahari tidak dapat diatur oleh manusia. Sedangkan tinggi tanaman
merupakan variabel dependen karena perubahan tinggi tanaman dipengaruhi
langsung oleh intensitas cahaya matahari sebagai variabel indipenden.
MACAM-MACAM KORELASI
Korelasi sebagai
sebuah analisis memiliki berbagai jenis menurut tingkatannya. Beberapa
tingkatan korelasi yang telah dikenal selama ini antara lain adalah korelasi
sederhana, korelasi parsial, dan korelasi ganda. Berikut ini adalah penjelasan
dari masing-masing korelasi dan bagaimana cara menghitung hubungan dari
masing-masing korelasi tersebut.
1. Korelasi Sederhana
Korelasi Sederhana
merupakan suatu teknik statistik yang dipergunakan untuk mengukur kekuatan
hubungan antara 2 variabel dan juga untuk dapat mengetahui bentuk hubungan
keduanya dengan hasil yang bersifat kuantitatif. Kekuatan hubungan antara 2
variabel yang dimaksud adalah apakah hubungan tersebut erat, lemah,
ataupun tidak erat. Sedangkan bentuk hubungannya adalah apakah bentuk
korelasinya linear positifataupun linear negatif.
Di antara sekian
banyak teknik-teknik pengukuran asosiasi, terdapat dua teknik korelasi yang
sangat populer sampai sekarang, yaitu Korelasi Pearson Product Moment dan
Korelasi Rank Spearman. Lalu apa perbedaan di antara keduanya?
Korelasi Pearson
Product Moment adalah korelasi yang digunakan untuk data kontinu dan data
diskrit. Korelasi pearson cocok digunakan untuk statistik parametrik. Ketika
data berjumlah besar dan memiliki ukuran parameter seperti mean dan standar
deviasi populasi.
Korelasi Pearson
menghitung korelasi dengan menggunakan variasi data. Keragaman data tersebut
dapat menunjukkan korelasinya. Korelasi ini menghitung data apa adanya, tidak
membuat ranking atas data yang digunakan seperti pada korelasi Rank Spearman.
Ketika kita memiliki data numerik seperti nilai tukar rupiah, data rasio
keuangan, tingkat pertumbuhan ekonomi, data berat badan dan contoh data numerik
lainnya, maka Korelasi Pearson Product Moment cocok digunakan.
Sebaliknya, Koefisien
Korelasi Rank Spearman digunakan untuk data diskrit dan kontinu namun untuk
statistik nonparametrik. Koefisien korelasi Rank Spearman lebih cocok untuk
digunakan pada statistik nonparametrik. Statistik nonparametrik adalah
statistik yang digunakan ketika data tidak memiliki informasi parameter, data
tidak berdistribusi normal atau data diukur dalam bentuk ranking. Berbeda
dengan Korelasi Pearson, korelasi ini tidak memerlukan asumsi normalitas, maka
korelasi Rank Spearman cocok juga digunakan untuk data dengan sampel
kecil.
Korelasi Rank
Spearman menghitung korelasi dengan menghitung ranking data terlebih dahulu.
Artinya korelasi dihitung berdasarkan orde data. Ketika peneliti berhadapan
dengan data kategorik seperti kategori pekerjaan, tingkat pendidikan, kelompok
usia, dan contoh data ketegorik lainnya, maka Korelasi Rank Spearman cocok
digunakan. Korelasi Rank Spearman pun cocok digunakan pada kondisi dimana
peneliti dihadapkan pada data numerik (kurs rupiah, rasio keuangan, pertumbuhan
ekonomi), namun peneliti tidak memiliki cukup banyak data (data kurang dari
30).
2. Korelasi Parsial
Korelasi parsial
adalah suatu metode pengukuran keeratan hubungan (korelasi) antara variabel
bebas dan variabel tak bebas dengan mengontrol salah satu variabel bebas untuk
melihat korelasi natural antara variabel yang tidak terkontrol. Analisis
korelasi parsial (partial correlation) melibatkan dua variabel. Satu buah variabel
yang dianggap berpengaruh akan dikendalikan atau dibuat tetap (sebagai variabel
kontrol).
Sebagai contoh
misalnya kita akan meneliti hubungan variabel X2 dan variabel bebas Y, denganX1
dikontrol (korelasi parsial). Disini variabel yang dikontrol (X1) dikeluarkan
atau dibuat konstan. Sehingga X2’ = X2 – (b2X1 + a2 ) dan Y’ = Y – (b1 X1 +a1
), tetapi nilai a dan b didapatkan dengan menggunakan regresi linear. Setelah
hasilnya diperoleh, kemudian dicari regresi X2‘ dengan Y’ dimana : Y’ = b3X2’
+a3. Korelasi yang didapatkan dan sejalan dengan model-model di atas dinamakan
korelasi parsial X2 dan Y sedangkan X1 dibuat konstan.
Nilai korelasi
berkisar antara 1 sampai -1, nilai semakin mendekati 1 atau -1 berarti hubungan
antara dua variabel semakin kuat. Sebaliknya, jika nilai mendekati 0 berarti
hubungan antara dua variabel semakin lemah. Nilai positif menunjukkan hubungan
searah (X naik, maka Y naik) sementara nilai negatif menunjukkan hubungan
terbalik (X naik, maka Y turun).
Data yang digunakan
dalam korelasi parsial biasanya memiliki skala interval atau rasio. Berikut
adalah pedoman untuk memberikan interpretasi serta analisis bagi koefisien
korelasi menurut Sugiyono:
0.00 - 0,199 = sangat
rendah
0,20 - 0,3999 =
rendah
0,40 - 0,5999 =
sedang
0,60 - 0,799 = kuat
0,80 - 1,000 = sangat
kuat
3. Korelasi Ganda
Korelasi ganda adalah
bentuk korelasi yang digunakan untuk melihat hubungan antara tiga atau lebih
variabel (dua atau lebih variabel independen dan satu variabel dependent.
Korelasi ganda berkaitan dengan interkorelasi variabel-variabel independen
sebagaimana korelasi mereka dengan variabel dependen.
Korelasi ganda adalah
suatu nilai yang memberikan kuatnya pengaruh atau hubungan dua variabel atau
lebih secara bersama-sama dengan variabel lain. Korelasi ganda merupakan
korelasi yang terdiri dari dua atau lebih variabel bebas (X1,X2,…..Xn) serta
satu variabel terikat (Y). Apabila perumusan masalahnya terdiri dari tiga
masalah, maka hubungan antara masing-masing variabel dilakukan dengan cara
perhitungan korelasi sederhana.
Korelasi ganda
memiliki koefisien korelasi, yakni besar kecilnya hubungan antara dua variabel
yang dinyatakan dalam bilangan. Koefisien Korelasi disimbolkan dengan huruf R.
Besarnya Koefisien Korelasi adalah antara -1; 0; dan +1.
Besarnya korelasi -1
adalah negatif sempurna yakni terdapat hubungan di antara dua variabel atau
lebih namun arahnya terbalik, +1 adalah korelasi yang positif sempurna (sangat
kuat) yakni adanya sebuah hubungan di antara dua variabel atau lebih tersebut,
sedangkan koefisien korelasi 0 dianggap tidak terdapat hubungan antara dua
variabel atau lebih yang diuji sehingga dapat dikatakan tidak ada hubungan sama
sekali.
Analisis Regresi
Sederhana, Ini Penjelasannya
29Jan By Hidayat Huang
Analisis Regresi
Sederhana adalah sebuah metode pendekatan untuk pemodelan hubungan antara satu
variabel dependen dan satu variabel independen. Dalam model regresi, variabel
independen menerangkan variabel dependennya. Dalam analisis regresi sederhana,
hubungan antara variabel bersifat linier, dimana perubahan pada variabel X akan
diikuti oleh perubahan pada variabel Y secara tetap. Sementara pada hubungan
non linier, perubahaan variabel X tidak diikuti dengan perubahaan variabel y
secara proporsional. seperti pada model kuadratik, perubahan x diikuti oleh
kuadrat dari variabel x. Hubungan demikian tidak bersifat linier.
Secara matematis model analisis regresi linier sederhana dapat digambarkan
sebagai berikut:
Y = A + BX + e
Y adalah variabel dependen atau respon
A adalah intercept atau konstanta
B adalah koefisien regresi atau slope
e adalah residual atau error
Secara praktis analisis regresi linier sederhana memiliki kegunaan sebagai
berikut:
1. Model regresi sederhana dapat digunakan untuk forecast atau memprediksi
nilai Y. Namun sebelum melakukan forecasting, terlebih dahulu harus dibuat
model atau persamaan regresi linier. Ketika model yang fit sudah terbentuk maka
model tersebut memiliki kemampuan untuk memprediksi nilai Y berdasarkan
variabel Y yang diketahui. Katakanlah sebuah model regresi digunakan untuk
membuat persamaan antara pendapatan (X) dan konsumsi (Y). Ketika sudah
diperoleh model yang fit antara pendapatan dengan konsumsi, maka kita dapat
memprediksi berapa tingkat konsumsi masyarakat ketika kita sudah mengetahui
pendapatan masyarakat.
2. Mengukur pengaruh variabel X terhadap variabel Y. Misalkan kita memiliki
satu serial data variabel Y, melalui analisis regresi linier sederhana kita
dapat membuat model variabel-variabel yang memiliki pengaruh terhadap variabel
Y. Hubungan antara variabel dalam analisis regresi bersifat kausalitas atau
sebab akibat. Berbeda halnya dengan analisis korelasi yang hanya melihat
hubungan asosiatif tanpa mengetahui apa variabel yang menjadi sebab dan apa
variabel yang menjadi akibat.
Model regresi linier sederhana yang baik harus memenuhi asumsi-asumsi berikut:
1. Eksogenitas yang lemah, kita harus memahami secara mendasar sebelum
menggunakan analisis regresi bahwa analisis ini mensyaratkan bahwa variabel X
bersifat fixed atau tetap, sementara variabel Y bersifat random. Maksudnya
adalah satu nilai variabel X akan memprediksi variabel Y sehingga ada
kemungkinan beberapa variabel Y. dengan demikian harus ada nilai error atau
kesalahan pada variabel Y. Sebagai contoh ketika pendapatan (X) seseorang
sebesar Rp 1 juta rupiah, maka pengeluarannya bisa saja, Rp 500 ribu, Rp 600
ribu, Rp 700 ribu dan seterusnya.
2. Linieritas, seperti sudah dijelaskan sebelumnya bahwa model analisis regresi
bersifat linier. artinya kenaikan variabel X harus diikuti secara proporsional
oleh kenaikan variabel Y. Jika dalam pengujian linieritas tidak terpenuhi, maka
kita dapat melakukan transformasi data atau menggunakan model kuadratik,
eksponensial atau model lainnya yang sesuai dengan pola hubungan non-linier.
3. Varians error yang konstan, ini menjelaskan bahwa varians error atau varians
residual yang tidak berubah-ubah pada respon yang berbeda. asumsi ini lebih
dikenal dengan asumsi homoskedastisitas. Mengapa varians error perlu konstan?
karena jika konstan maka variabel error dapat membentuk model sendiri dan
mengganggu model. Oleh karena itu, penanggulangan permasalahan
heteroskedastisitas/non-homoskedastisitas dapat diatasi dengan menambahkan
model varians error ke dalam model atau model ARCH/GARCH.
4. Autokorelasi untuk data time series, jika kita menggunakan analisis regresi
sederhana untuk data time series atau data yang disusun berdasarkan urutan
waktu, maka ada satu asumsi yang harus dipenuhi yaitu asumsi autokorelasi.
Asumsi ini melihat pengaruh variabel lag waktu sebelumnya terhadap variabel Y.
Jika ada gangguan autokorelasi artinya ada pengaruh variabel lag waktu
sebelumnya terhadap variabel Y. sebagai contoh, model kenaikan harga BBM
terhadap inflasi, jika ditemukan atukorelasi artinya terdapat pengaruh lag
waktu terhadap inflasi. Artinya inflasi hari ini atau bulan ini bukan
dipengaruhi oleh kenaikan BBM hari ini namun dipengaruhi oleh kenaikan BBM
sebelumnya (satu hari atau satu bulan tergantung data yang dikumpulkan).
Analisis regresi
linier sederhana adalah hubungan secara linear antara satu variabel independen
(X) dengan variabel dependen (Y). Analisis ini untuk mengetahui arah hubungan
antara variabel independen dengan variabel dependen apakah positif atau negatif
dan untuk memprediksi nilai dari variabel dependen apabila nilai variabel
independen mengalami kenaikan atau penurunan.. Data yang digunakan biasanya
berskala interval atau rasio.
Rumus regresi linear
sederhana sebagi berikut:
Y’ = a + bX
Keterangan:
Y’ = Variabel
dependen (nilai yang diprediksikan)
X =
Variabel independen
a =
Konstanta (nilai Y’ apabila X = 0)
b =
Koefisien regresi (nilai peningkatan ataupun penurunan)
Contoh kasus:
Seorang mahasiswa
bernama Hermawan ingin meneliti tentang pengaruh biaya promosi terhadap volume
penjualan pada perusahaan jual beli motor. Dengan ini di dapat variabel
dependen (Y) adalah volume penjualan dan variabel independen (X) adalah biaya
promosi. Dengan ini Hermawan menganalisis dengan bantuan program SPSS dengan
alat analisis regresi linear sederhana. Data-data yang di dapat ditabulasikan
sebagai berikut:
Tabel. Tabulasi
Data Penelitian (Data Fiktif)
|
No
|
Biaya Promosi
|
Volume Penjualan
|
|
1
|
12,000
|
56,000
|
|
2
|
13,500
|
62,430
|
|
3
|
12,750
|
60,850
|
|
4
|
12,600
|
61,300
|
|
5
|
14,850
|
65,825
|
|
6
|
15,200
|
66,354
|
|
7
|
15,750
|
65,260
|
|
8
|
16,800
|
68,798
|
|
9
|
18,450
|
70,470
|
|
10
|
17,900
|
65,200
|
|
11
|
18,250
|
68,000
|
|
12
|
16,480
|
64,200
|
|
13
|
17,500
|
65,300
|
|
14
|
19,560
|
69,562
|
|
15
|
19,000
|
68,750
|
|
16
|
20,450
|
70,256
|
|
17
|
22,650
|
72,351
|
|
18
|
21,400
|
70,287
|
|
19
|
22,900
|
73,564
|
|
20
|
23,500
|
75,642
|
Langkah-langkah pada
program SPSS
Ø Masuk
program SPSS
Ø Klik
variable view pada SPSS data editor
Ø Pada
kolom Name ketik y, kolom Name pada baris kedua ketik x.
Ø Pada
kolom Label, untuk kolom pada baris pertama ketik Volume Penjualan, untuk kolom
pada baris kedua ketik Biaya Promosi.
Ø Untuk
kolom-kolom lainnya boleh dihiraukan (isian default)
Ø Buka
data view pada SPSS data editor, maka didapat kolom variabel y dan x.
Ø Ketikkan
data sesuai dengan variabelnya
Ø Klik
Analyze - Regression - Linear
Ø Klik
variabel Volume Penjualan dan masukkan ke kotak Dependent, kemudian klik
variabel Biaya Promosi dan masukkan ke kotak Independent.
Ø Klik
Statistics, klik Casewise diagnostics, klik All cases. Klik Continue
Ø Klik OK, maka
hasil output yang didapat pada kolom Coefficients dan Casewise Diagnostics
adalah sebagai berikut:
Tabel.
Hasil Analisis Regresi Linear Sederhana


Persamaan regresinya
sebagai berikut:
Y’ = a + bX
Y’
= -28764,7 + 0,691X
Angka-angka ini dapat
diartikan sebagai berikut:
- Konstanta sebesar
-28764,7; artinya jika biaya promosi (X) nilainya adalah 0, maka volume
penjulan (Y’) nilainya negatif yaitu sebesar -28764,7.
- Koefisien
regresi variabel harga (X) sebesar 0,691; artinya jika harga mengalami kenaikan
Rp.1, maka volume penjualan (Y’) akan mengalami peningkatan sebesar Rp.0,691.
Koefisien bernilai positif artinya terjadi hubungan positif antara harga dengan
volume penjualan, semakin naik harga maka semakin meningkatkan volume
penjualan.
Nilai volume
penjualan yang diprediksi (Y’) dapat dilihat pada tabel Casewise Diagnostics
(kolom Predicted Value). Sedangkan Residual (unstandardized residual) adalah
selisih antara Volume Penjualan dengan Predicted Value, dan Std. Residual
(standardized residual) adalah nilai residual yang telah terstandarisasi (nilai
semakin mendekati 0 maka model regresi semakin baik dalam melakukan prediksi,
sebaliknya semakin menjauhi 0 atau lebih dari 1 atau -1 maka semakin tidak baik
model regresi dalam melakukan prediksi).
- Uji
Koefisien Regresi Sederhana (Uji t)
Uji ini digunakan
untuk mengetahui apakah variabel independen (X) berpengaruh secara signifikan
terhadap variabel dependen (Y). Signifikan berarti pengaruh yang terjadi dapat
berlaku untuk populasi (dapat digeneralisasikan).
Dari hasil analisis
regresi di atas dapat diketahui nilai t hitung seperti pada tabel 2.
Langkah-langkah pengujian sebagai berikut:
1. Menentukan
Hipotesis
Ho : Ada
pengaruh secara signifikan antara biaya promosi dengan volume penjualan
Ha
: Tidak ada pengaruh secara signifikan antara biaya
promosi dengan volume penjualan
2. Menentukan
tingkat signifikansi
Tingkat signifikansi
menggunakan a = 5% (signifikansi 5% atau 0,05 adalah ukuran standar
yang sering digunakan dalam penelitian)
3. Menentukan
t hitung
Berdasarkan
tabel diperoleh t hitung sebesar 10,983
4. Menentukan
t tabel
Tabel distribusi t
dicari pada a = 5% : 2 = 2,5% (uji 2 sisi) dengan derajat kebebasan
(df) n-k-1 atau 20-2-1 = 17 (n adalah jumlah kasus dan k
adalah jumlah variabel independen). Dengan pengujian 2 sisi (signifikansi =
0,025) hasil diperoleh untuk t tabel sebesar 2,110 (Lihat pada lampiran) atau
dapat dicari di Ms Excel dengan cara pada cell kosong ketik =tinv(0.05,17) lalu
enter.
5. Kriteria
Pengujian
Ho diterima jika –t
tabel < t hitung < t tabel
Ho
ditolak jika -thitung < -t tabel atau t hitung > t tabel
6. Membandingkan
t hitung dengan t tabel
Nilai t hitung > t
tabel (10,983 > 2,110) maka Ho ditolak.
7. Kesimpulan
Oleh karena nilai t
hitung > t tabel (10,983 > 2,110) maka Ho ditolak, artinya bahwa ada
pengaruh secara signifikan antara biaya promosi dengan volume penjualan. Jadi
dalam kasus ini dapat disimpulkan bahwa biaya promosi berpengaruh terhadap
volume penjualan pada perusahaan jual beli motor.
Regresi linier
berganda merupakan salah satu pengujian hipotesis untuk mengetahui pengaruh
antara variabel bebas (independen) terhadap variabel tetapnya (dependen).
Selain itu uji hipotesis yang lainnya adalah Uji T, Uji F dan Uji R² yang akan
di bahas dalam artikel ini… Secara tajam, setajam…….. Pisau dapur..!! Hehehe..
Okedeh, tanpa basa
basi saya antar anda kepada pembahasannya. Dijamin akan sangat bermanfaat..
1. Analisis Regresi
Linier Berganda
Analisis regresi
linier berganda ini digunakan untuk mengetahui ada tidaknya pengaruh dari
variabel bebas terhadap variabel terikat. Disini saya akan memberikan contoh
seperti artikel saya sebelumnya, lihat artikelnya disini.
Sehingga yang saya
cari adalah pengaruh variabel bebas (independen variable)
yaitu Leverage (X1), CR (X2), Return On
Asset (X3) dan Return On Equity (X4) terhadap variabel terikat
(dependen variable) yaitu Beta (Y).
Dan persamaan
regresinya dapat dirumuskan sebagai berikut (Suharyadi dan Purwanto, 2004:509):

Dimana:
Y
= Beta (β)
a
= Konstanta
b1,b2,b3,b4 =
Koefisien determinasi
X1
= Leverage
X2
= CR
X3
= Return On Asset (ROA)
X4
= Return On Equity (ROE)
e
= Error
Untuk membaca dari
hasil SPSS terhadap persamaan regresinya adalah dengan melihat output spss pada
tabel “Coefficients” (yang
belum tau caranya bisa dilihat langkahnya dengan klik disini).
Untuk lebih jelasnya
bisa lihat pada contoh
saya yang sebelumnya dan gambar di bawah ini:

Berdasarkan tabel
diatas dapat diperoleh rumus regresi sebagai berikut:
Y = (-0,094) + 2,934
X1 – 0,071 X2 – 0,043 X3 – 0,003 X4 + e
Interpretasi dari
regresi diatas adalah sebagai berikut:
1. Konstanta (a)
Ini berarti jika
semua variabel bebas memiliki nilai nol (0) maka nilai variabel terikat (Beta)
sebesar -0,094.
2. Leverage (X1)
terhadap beta (Y)
Nilai koefisien
Leverage untuk variabel X1 sebesar 2,839. Hal ini mengandung arti bahwa setiap kenaikan
Leverage satu satuan maka variabel Beta (Y) akan naik sebesar 2,839 dengan
asumsi bahwa variabel bebas yang lain dari model regresi adalah tetap.
3. CR (X2) terhadap
beta (Y)
Nilai koefisien
Current Ratio untuk variabel X2 sebesar 0,071 dan bertanda negatif, ini
menunjukkan bahwa Current Ratio mempunyai hubungan yang berlawanan arah dengan
Risiko Sistematis. Hal ini mengandung arti bahwa setiap kenaikan Current Ratio
satu satuan maka variabel Beta (Y) akan turun sebesar 0,071 dengan asumsi bahwa
variabel bebas yang lain dari model regresi adalah tetap.
4. ROA (X3) terhadap
Beta (Y)
Nilai koefisien ROA
terstandarisasi untuk variabel X3 sebesar 0,043 dan bertanda negatif, ini
menunjukkan bahwa ROA mempunyai hubungan yang berlawanan arah dengan Risiko Sistematis.
Hal ini mengandung arti bahwa setiap kenaikan ROA satu satuan maka variabel
Beta (Y) akan turun sebesar 0,043 dengan asumsi bahwa variabel bebas yang lain
dari model regresi adalah tetap.
5. ROE (X4) terhadap
Beta (Y)
Nilai koefisien
ROE untuk variabel X4 sebesar 0,003 dan bertanda negatif, ini
menunjukkan bahwa ROE mempunyai hubungan yang berlawanan arah dengan Risiko
Sistematis. Hal ini mengandung arti bahwa setiap kenaikan ROE satu satuan maka
variabel Beta (Y) akan turun sebesar 0,003 dengan asumsi bahwa variabel bebas
yang lain dari model regresi adalah tetap.
2. Uji t
Uji t digunakan untuk
mengetahui apakah variabel-variabel independen secara parsial berpengaruh nyata
atau tidak terhadap variabel dependen. Derajat signifikansi yang digunakan
adalah 0,05. Apabila nilai signifikan lebih kecil dari derajat kepercayaan maka
kita menerima hipotesis alternatif, yang menyatakan bahwa suatu variabel
independen secara parsial mempengaruhi variabel dependen.
Analisis uji t juga
dilihat dari tabel ”Coefficient”. Contoh dari artikel saya sebelumnya:

Cara bacanya:
1. Leverage (X1)
terhadap Beta (Y)
Terlihat pada
kolom Coefficients model 1 terdapat nilai sig 0,002. Nilai sig lebih
kecil dari nilai probabilitas 0,05, atau nilai 0,002<0,05, maka
H1 diterima dan Ho ditolak. Variabel X1 mempunyai
thitung yakni 3,317 dengan ttabel=2,021. Jadi
thitung>ttabel dapat disimpulkan bahwa variabel X1 memiliki
kontribusi terhadap Y. Nilai t positif menunjukkan bahwa variabel
X1 mempunyai hubungan yang searah dengan Y. Jadi dapat disimpulkan
leverage memiliki pengaruh signifikan terhadap Beta.
2. Current Ratio (X2)
terhadap beta (Y)
Terlihat pada
kolom Coefficients model 1 terdapat nilai sig 0,039. Nilai sig lebih
kecil dari nilai probabilitas 0,05, atau nilai 0,039<0,05, maka
H1 diterima dan Ho ditolak. Variabel X2 mempunyai
thitung yakni 2,134 dengan ttabel=2,021. Jadi
thitung>ttabel dapat disimpulkan bahwa variabel X2 memiliki
kontribusi terhadap Y. Nilai t negatif menunjukkan bahwa X2 mempunyai
hubungan yang berlawanan arah dengan Y. Jadi dapat disimpulkan CR
memiliki pengaruh signifikan terhadap beta.
3. ROA (X3) terhadap
Beta (Y)
Terlihat nilai sig
untuk ROA adalah 0,100. Nilai sig lebih besar dari nilai probabilitas 0,05,
atau nilai 0,100>0,05, maka H1 ditolak dan Ho diterima. Variabel
X3mempunyai thitung yakni 1,683 dengan ttabel=2,021. Jadi
thitung<ttabel dapat disimpulkan bahwa variabel X3 tidak memiliki
kontribusi terhadap Y. Nilai t negatif menunjukkan bahwa X3 mempunyai
hubungan yang berlawanan arah dengan Y. Jadi dapat disimpulkan ROA tidak
berpengaruh signifikan terhadap risiko Beta
.
4. ROE (X4) terhadap
Terlihat nilai sig
pada ROE adalah 0,726. Nilai sig lebih besar dari nilai probabilitas 0,05, atau
nilai 0,726>0,05, maka H1 ditolak dan Ho diterima. Variabel X4mempunyai
thitung yakni 0,353 dengan ttabel=2,021. Jadi
thitung<ttabel dapat disimpulkan bahwa variabel X4 tidak memiliki
kontribusi terhadap Y. Nilai t negatif menunjukkan bahwa ROE mempunyai hubungan
yang berlawanan arah dengan Beta. Jadi dapat disimpulkan ROE tidak berpengaruh
signifikan terhadap risiko Beta.
Sehingga ringkasan
hasil pengujian hipotesis adalah sbb:

3. Uji F
Uji F digunakan untuk
mengetahui apakah variabel-variabel independen secara simultan berpengaruh
signifikan terhadap variabel dependen. Derajat kepercayaan yang digunakan
adalah 0,05. Apabila nilai F hasil perhitungan lebih besar daripada nilai F
menurut tabel maka hipotesis alternatif, yang menyatakan bahwa semua variabel
independen secara simultan berpengaruh signifikan terhadap variabel dependen.
Untuk analisisnya
dari output SPSS dapat dilihat dari tabel ”Anova”, seperti contoh saya:

Cara bacanya:
Pengujian secar
simultan X1, X2, X3 dan X4 terhadap Y:
Dari tabel diperoleh
nilai Fhitung sebesar 5,889 dengan nilai probabilitas (sig)=0,001. Nilai
Fhitung (5,889)>Ftabel (2,61), dan nilai sig. lebih kecil dari
nilai probabilitas 0,05 atau nilai 0,001<0,05; maka H01 diterima,
berarti secara bersama-sama (simultan) Leverage, CR, ROA dan ROE berpengaruh
signifikan terhadap Beta. ditolak dan H
4. Koefisien
determinasi (R²)
Koefisien determinasi
digunakan untuk mengetahui seberapa besar hubungan dari beberapa variabel dalam
pengertian yang lebih jelas. Koefisien determinasi akan menjelaskan seberapa
besar perubahan atau variasi suatu variabel bisa dijelaskan oleh perubahan atau
variasi pada variabel yang lain (Santosa&Ashari, 2005:125).
Dalam bahasa
sehari-hari adalah kemampuan variabel bebas untuk berkontribusi terhadap
variabel tetapnya dalam satuan persentase.
Nilai koefisien ini antara
0 dan 1, jika hasil lebih mendekati angka 0 berarti kemampuan variabel-variabel
independen dalam menjelaskan variasi variabel amat terbatas. Tapi jika hasil
mendekati angka 1 berarti variabel-variabel independen memberikan hampir semua
informasi yang dibutuhkan untuk memprediksi variasi variabel dependen.
Untuk analisisnya
dengan menggunakan output SPSS dapat dilihat pada tabel ”Model Summary”.
Supaya lebih
sederhana lihat contoh saya berikut ini:

Cara bacanya
(berdasarkan contoh saya sebelumnya):
Berdasarkan Tabel
”Model Summary” dapat disimpulkan bahwa Leverage, CR, ROA dan ROE berpengaruh
sebesar 35,4% terhadap Risiko Sistematis, sedangkan 64,6% dipengaruhi variabel
lain yang tidak diteliti. Karena nilai R Square dibawah 5% atau cenderung
mendekati nilai 0 maka dapat disimpulkan kemampuan variabel-variabel
independen dalam menjelaskan variasi variabel amat terbatas.
Demikian penjelasan
dari saya. Semoga bermanfaat bagi kita semua. Jangan lupa lihat link Contoh
Cara Analisis Data Dengan SPSS yang bisa di lihat denganklik
disini. Atau jika tidak bisa bisa copy paste link ini di jendela baru:
Salam,
Persamaan Model
Regresi Linear
Model persamaan
regresi sering kali digunakan dalam metode penelitian. Sebenarnya ada perbedaan
antara model regresi dengan persamaan regresi. Namun sering kali peneliti belum
mengetahui perbedaan itu. Nah mari kita lihat berikut ini:
Y = a + bX ⇒
yang ini namanya persamaan
Yt= a+bXt ⇒
yang ini namanya model
Sekarang teman-teman tahu kan mana persamaan mana model. Kegunaannya juga
berbeda. Ilmu social dengan penelitian terkait dengan data primer menggunakan
persamaan regresi sedangkan ilmu eksak dengan penelitian terkait dengan data
sekunder menggunakan model regresi. Meskipun tidak menutup kemungkinan kedua
ilmu tersebut menggunakan keduanya/kebalikannya.
Persamaan regresi memiliki makna lebih keintrepretasi hasil pada saat
pengambilan data. Sehingga hasilnya hanya mampu menggambarkan kejadian saat itu
dengan sampel pada saat itu pula. Oleh karena itu, penelitian pada ilmu social
tidak dapat diartikan sama halnya dengan ilmu eksak dalam mengintrepretasi
hasil persamaan regresi. Terkadang baik peneliti maupun pembimbing peneliti
tidak menghiraukan penggunaan Unstandardized dan Standardized
|
Unstandardized
Coeficients
|
Standardized
Coeficients
|
||||
|
Model
|
B
|
Std.Error
|
Beta
|
t
|
Sig.
|
|
1(constant)
|
6.229
|
.446
|
13.960
|
.000
|
|
|
AFEKTIF
|
-.731
|
.088
|
-.621
|
-.8258
|
.000
|
|
CONTINUANCE
|
-.077
|
.098
|
-.059
|
-.779
|
.437
|
|
NORMATIF
|
-.153
|
.108
|
-.111
|
-.1419
|
-.159
|
a. Dependent
Variable: TURNOVER INTENTIONS Masing-masing memiliki fungsi dan kegunaan
sesuai dengan data penelitian. Kebanyakan buku statistic hanya membahas
mengenai Unstandardized. Lalu bagaimana dengan yang Standardized? Nah
itu dia masalahnya, peneliti kurang menyadari akan makna persamaan dan
model.
- Unstandardized biasa digunakan untuk model regresi dimana fungsinya adalah untuk meramalkan gambaran masa depan dengan data masa lalu, sedangkan
- Standardized biasa digunakan untuk persamaan regresi dimana fungsinya adalah untuk mengetahui pengaruh dan sumbangan efektif yang diberikan antara variabel independen terhadap dependen, namun hanya berlaku pada saat itu dengan sampel itu.
Sekarang sudah tahu
kan mengapa ada dua beta dalam alat statistik regresi linear. Untuk kegunaannya
mau pilih yang mana monggo dikembalikan lagi kepada peneliti dan dosen
pembimbing sebab tidak semua peneliti dan dosen pembimbing yang tahu perbedaan ini.
Jika kasusnya seperti ini maka saran saya adalah ikutilah tradisi yang ada pada
kampusmu agar kamu cepat selesai SKRIPSI, TESISI mu hehehehehe.
Ada kasus lagi nih teman-teman. Terkadang hasil penelitian tidak sesuai dengan
teori yang ada sedangkan dosen atau dari dirimu menginginkan kesamaan agar
tidak rempong saat dicerca pertanyaan dalam sidang. Hal ini dapat diatasi
dengan melihat terlebih dahulu kesalahan apa yang ada pada data sehingga
hasilnya menyimpang. Bukankah teori yang dibuat tidak hanya berdasarkan logika
akan tetapi juga melewati tahap penelitian para ahli iya gak bro. Mari kita
tengok terlebih dahulu data kamu.
- Untuk alat statistic dengan metode regresi dapat dilihat dahulu apakah data sudah memenuhi asumsi?
- Apakah terdapat data outlier?
Uji Validitas
Validitas berasal dari kata validity yang mempunyai arti sejauh mana
ketepatan dan kecermatan suatu alat ukur dalam melakukam fungsi ukurannya
(Azwar 1986). Selain itu validitas adalah suatu ukuran yang menunjukkan bahwa
variabel yang diukur memang benar-benar variabel yang hendak diteliti oleh
peneliti (Cooper dan Schindler, dalam Zulganef, 2006).
Sedangkan menurut Sugiharto dan Sitinjak (2006), validitas berhubungan dengan
suatu peubah mengukur apa yang seharusnya diukur. Validitas dalam penelitian
menyatakan derajat ketepatan alat ukur penelitian terhadap isi sebenarnya yang
diukur. Uji validitas adalah uji yang digunakan untuk menunjukkan sejauh mana
alat ukur yang digunakan dalam suatu mengukur apa yang diukur. Ghozali (2009)
menyatakan bahwa uji validitas digunakan untuk mengukur sah, atau valid
tidaknya suatu kuesioner. Suatu kuesioner dikatakan valid jika pertanyaan pada
kuesioner mampu untuk mengungkapkan sesuatu yang akan diukur oleh kuesioner
tersebut.
Suatu tes dapat dikatakan memiliki validitas yang tinggi jika tes tersebut
menjalankan fungsi ukurnya, atau memberikan hasil ukur yang tepat dan
akurat sesuai dengan maksud dikenakannya tes tersebut. Suatu tes menghasilkan
data yang tidak relevan dengan tujuan diadakannya pengukuran dikatakan sebagai
tes yang memiliki validitas rendah.
Sisi lain dari pengertian validitas adalah aspek kecermatan pengukuran. Suatu
alat ukur yang valid dapat menjalankan fungsi ukurnya dengan tepat, juga
memiliki kecermatan tinggi. Arti kecermatan disini adalah dapat mendeteksi
perbedaan-perbedaan kecil yang ada pada atribut yang diukurnya.
Dalam pengujian validitas terhadap kuesioner, dibedakan menjadi 2, yaitu
validitas faktor dan validitas item. Validitas faktor diukur bila item yang
disusun menggunakan lebih dari satu faktor (antara faktor satu dengan yang lain
ada kesamaan). Pengukuran validitas faktor ini dengan cara mengkorelasikan
antara skor faktor (penjumlahan item dalam satu faktor) dengan skor total
faktor (total keseluruhan faktor).
Validitas item ditunjukkan dengan adanya korelasi atau dukungan terhadap item
total (skor total), perhitungan dilakukan dengan cara mengkorelasikan antara
skor item dengan skor total item. Bila kita menggunakan lebih dari satu faktor
berarti pengujian validitas item dengan cara mengkorelasikan antara skor item
dengan skor faktor, kemudian dilanjutkan mengkorelasikan antara skor item
dengan skor total faktor (penjumlahan dari beberapa faktor).
Dari hasil perhitungan korelasi akan didapat suatu koefisien korelasi yang digunakan
untuk mengukur tingkat validitas suatu item dan untuk menentukan apakah suatu
item layak digunakan atau tidak. Dalam penentuan layak atau tidaknya suatu item
yang akan digunakan, biasanya dilakukan uji signifikansi koefisien korelasi
pada taraf signifikansi 0,05, artinya suatu item dianggap valid jika
berkorelasi signifikan terhadap skor total.
Untuk melakukan uji validitas ini menggunakan program SPSS. Teknik
pengujian yang sering digunakan para peneliti untuk uji validitas adalah
menggunakan korelasi Bivariate Pearson (Produk Momen Pearson).
Analisis ini dengan cara mengkorelasikan masing-masing skor item dengan skor
total. Skor total adalah penjumlahan dari keseluruhan item. Item-item
pertanyaan yang berkorelasi signifikan dengan skor total menunjukkan item-item
tersebut mampu memberikan dukungan dalam mengungkap apa yang ingin diungkap à
Valid. Jika r hitung ≥ r tabel (uji 2 sisi dengan sig. 0,05) maka instrumen
atau item-item pertanyaan berkorelasi signifikan terhadap skor total
(dinyatakan valid). Langkah-langkah dalam pengujian validitas ini yaitu :
1. Buat skor total masing-masing variabel (Tabel perhitungan skor)

2. Klik Analyze -> Correlate -> Bivariate
(Gambar/Output SPSS)

3. Masukan seluruh item variabel x ke Variabels

4. Cek list Pearson ; Two Tailed ; Flag
5. Klik Ok
Tabel rangkuman hasil uji validitas dari variabel tersebut dapat dilihat
sebagai berikut :

Dari tabel diatas dapat dijelaskan bahwa nilai r hitung > r tabel
berdasarkan uji signifikan 0.05, artinya bahwa item-item tersebut diatas valid
Rumus Korelasi Product Moment :
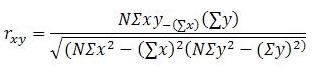
Keterangan :

Uji Reliabilitas
Reliabilitas berasal dari kata reliability. Pengertian dari reliability
(rliabilitas) adalah keajegan pengukuran (Walizer, 1987). Sugiharto dan
Situnjak (2006) menyatakan bahwa reliabilitas menunjuk pada suatu pengertian
bahwa instrumen yang digunakan dalam penelitian untuk memperoleh informasi yang
digunakan dapat dipercaya sebagai alat pengumpulan data dan mampu mengungkap
informasi yang sebenarnya dilapangan. Ghozali (2009) menyatakan bahwa
reliabilitas adalah alat untuk mengukur suatu kuesioner yang merupakan
indikator dari peubah atau konstruk. Suatu kuesioner dikatakan reliabel atau
handal jika jawaban seseorang terhadap pernyataan adalah konsisten atau stabil dari
waktu ke waktu. Reliabilitas suatu test merujuk pada derajat stabilitas,
konsistensi, daya prediksi, dan akurasi. Pengukuran yang memiliki reliabilitas
yang tinggi adalah pengukuran yang dapat menghasilkan data yang reliabel
Menurut Masri Singarimbun, realibilitas adalah indeks yang menunjukkan sejauh
mana suatu alat ukur dapat dipercaya atau dapat diandalkan. Bila suatu alat
pengukur dipakai dua kali – untuk mengukur gejala yang sama dan hasil
pengukuran yang diperoleh relative konsisten, maka alat pengukur tersebut
reliable. Dengan kata lain, realibitas menunjukkan konsistensi suatu alat
pengukur di dalam pengukur gejala yang sama.
Menurut Sumadi Suryabrata (2004: 28) reliabilitas menunjukkan sejauhmana hasil
pengukuran dengan alat tersebut dapat dipercaya. Hasil pengukuran harus
reliabel dalam artian harus memiliki tingkat konsistensi dan kemantapan.
Reliabilitas, atau keandalan, adalah konsistensi dari serangkaian pengukuran
atau serangkaian alat ukur. Hal tersebut bisa berupa pengukuran dari alat ukur
yang sama (tes dengan tes ulang) akan memberikan hasil yang sama, atau untuk
pengukuran yang lebih subjektif, apakah dua orang penilai memberikan skor yang
mirip (reliabilitas antar penilai). Reliabilitas tidak sama dengan validitas.
Artinya pengukuran yang dapat diandalkan akan mengukur secara konsisten, tapi
belum tentu mengukur apa yang seharusnya diukur. Dalam penelitian, reliabilitas
adalah sejauh mana pengukuran dari suatu tes tetap konsisten setelah dilakukan
berulang-ulang terhadap subjek dan dalam kondisi yang sama. Penelitian dianggap
dapat diandalkan bila memberikan hasil yang konsisten untuk pengukuran yang
sama. Tidak bisa diandalkan bila pengukuran yang berulang itu memberikan hasil
yang berbeda-beda.
Tinggi rendahnya reliabilitas, secara empirik ditunjukan oleh suatu angka yang
disebut nilai koefisien reliabilitas. Reliabilitas yang tinggi ditunjukan
dengan nilai rxx mendekati angka 1. Kesepakatan secara umum reliabilitas yang
dianggap sudah cukup memuaskan jika ≥ 0.700.
Pengujian reliabilitas instrumen dengan menggunakan rumus Alpha Cronbach karena
instrumen penelitian ini berbentuk angket dan skala bertingkat. Rumus Alpha
Cronbach sevagai berikut :

Keterangan :

Jika nilai alpha > 0.7 artinya reliabilitas mencukupi (sufficient
reliability) sementara jika alpha > 0.80 ini mensugestikan seluruh item
reliabel dan seluruh tes secara konsisten memiliki reliabilitas yang kuat.
Atau, ada pula yang memaknakannya sebagai berikut:
Jika alpha > 0.90 maka reliabilitas sempurna. Jika alpha antara 0.70 – 0.90
maka reliabilitas tinggi. Jika alpha 0.50 – 0.70 maka reliabilitas moderat.
Jika alpha < 0.50 maka reliabilitas rendah. Jika alpha rendah, kemungkinan
satu atau beberapa item tidak reliabel.
Langkah pengujian reliabilitas dengan SPSS :
- Klik Analyze -> Scale -> Reliability Analysis
- Masukan seluruh item variabel X ke Items

3.Pastikan pada model terpilih Alpha
4. Klik Ok

Nilai Cronbach Alpha sebesar 0.981 yang menunjukan bahwa ke-11 pernyataan cukup
reliabel


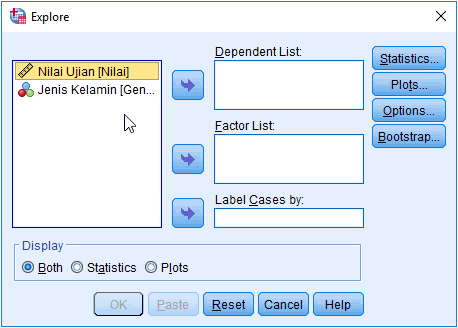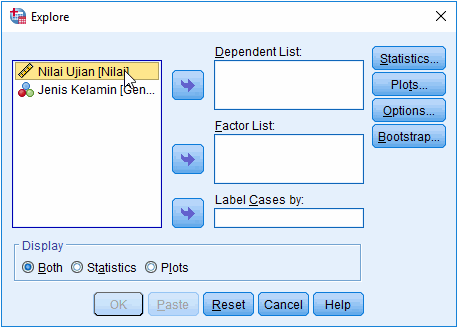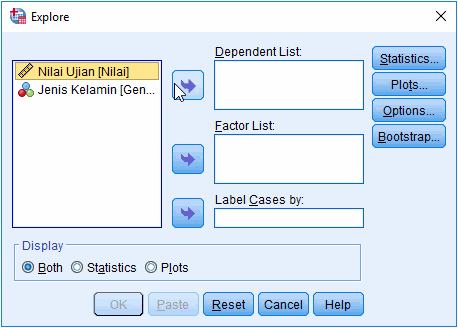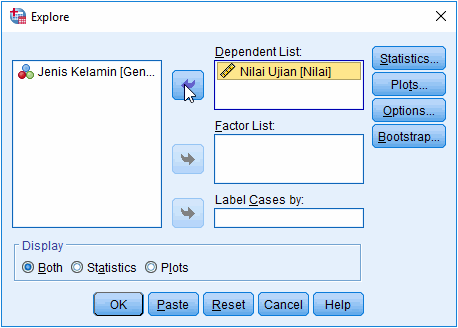

0 komentar:
Posting Komentar